| Rank | Theorem | Name |
| 6 | Thm*  k: k: , f:( , f:( k inj k inj  k). k).  i: i:  . .  u: u: k. f{ k. f{ i}(u) = u i}(u) = u | [iter_perm_cycles_uniform] |
| cites the following: |
| 4 | Thm*  k: k: , f:( , f:( k inj k inj  k), u: k), u: k. k.  i: i:  . f{ . f{ i}(u) = u i}(u) = u | [compose_iter_inj_cycles] |
| 0 | Thm*  k: k: , Q:( , Q:( k k  A A  Prop). Prop).
Thm* ( x: x: k. k.  y:A. Q(x;y)) y:A. Q(x;y))   ( ( f:( f:( k k  A). A).  x: x: k. Q(x;f(x))) k. Q(x;f(x))) | [finite_choice] |
| 5 | Thm*  a,b: a,b: , e:({a..b , e:({a..b } }   ), i:{a..b ), i:{a..b }. e(i) | ( }. e(i) | (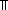 i:{a..b i:{a..b }. e(i)) }. e(i)) | [components_divide_iter_mul] |
| 2 | Thm*  a,b: a,b: . a | b . a | b   ( ( c: c: . b = a . b = a c) c) | [divides_def_on_nat] |
| 3 | Thm*  x,y: x,y:  . x . x y y    | [mul_nat_plus] |
| 4 | Thm*  x:A, f:(A x:A, f:(A  A), i,j,k: A), i,j,k: . k = i . k = i j j   f{ f{ i}{ i}{ j}(x) = f{ j}(x) = f{ k}(x) k}(x)  A A | [compose_iter_prod] |
| 1 | Thm*  f:(A f:(A  A), u:A. f(u) = u A), u:A. f(u) = u   ( ( i: i: . f{ . f{ i}(u) = u) i}(u) = u) | [compose_iter_point_id] |