| | Who Cites Formula? |
|
| Formula | Def Formula == rec(formula.Var+formula+(formula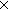 formula)+(formula formula)+(formula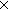 formula)+(formula formula)+(formula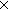 formula)) formula)) |
| | | Thm* Formula 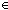 Type Type |
|
| Var | Def Var == Atom |
| | | Thm* Var 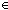 Type Type |
|
| f_or | Def p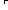 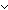 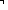 q == inr(inr(inr(inl( < p,q > )))) q == inr(inr(inr(inl( < p,q > )))) |
| | | Thm*  p,q:Formula. p p,q:Formula. p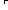 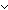 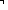 q q 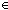 Formula Formula |
|
| fand | Def p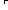 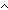 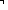 q == inr(inr(inl( < p,q > ))) q == inr(inr(inl( < p,q > ))) |
| | | Thm*  p,q:Formula. p p,q:Formula. p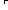 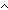 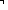 q q 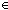 Formula Formula |
|
| fimp | Def p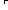 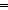 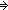 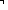 q == inr(inr(inr(inr( < p,q > )))) q == inr(inr(inr(inr( < p,q > )))) |
| | | Thm*  p,q:Formula. p p,q:Formula. p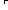 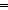 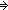 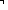 q q 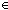 Formula Formula |
|
| fnot | Def 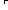 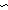 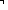 p == inr(inl(p)) p == inr(inl(p)) |
| | | Thm*  x:Formula. x:Formula. 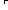 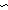 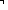 x x 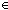 Formula Formula |
|
| formula_rank | Def 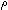 == (letrec formula_rank f = case f: == (letrec formula_rank f = case f: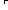 x x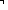 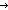 0; 0;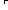 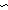 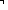 p p 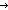 (formula_rank(p)+1);p (formula_rank(p)+1);p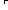 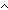 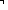 q q 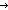 (formula_rank(p)+formula_rank(q)+1);p (formula_rank(p)+formula_rank(q)+1);p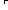 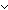 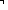 q q 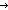 (formula_rank(p)+formula_rank(q)+1);p (formula_rank(p)+formula_rank(q)+1);p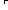 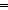 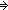 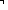 q q 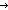 (formula_rank(p)+formula_rank(q)+1); ) (formula_rank(p)+formula_rank(q)+1); ) |
| | | Thm* 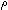 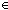 Formula Formula 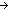 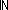 |
|
| formula_case | Def case F: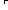 x x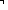 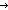 varC(x); varC(x);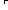 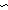 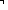 p1 p1 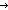 notC(p1);p2 notC(p1);p2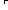 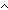 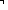 p3 p3 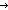 andC(p2;p3);p4 andC(p2;p3);p4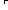 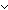 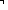 p5 p5 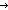 orC(p4;p5);p6 orC(p4;p5);p6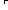 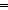 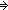 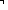 p7 p7 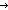 impC(p6;p7); == InjCase(F; x. varC(x); F. InjCase(F; p1. notC(p1); F. InjCase(F; x. x/p2,p3. andC(p2;p3); F. InjCase(F; x. x/p4,p5. orC(p4;p5), x/p6,p7. impC(p6;p7))))) impC(p6;p7); == InjCase(F; x. varC(x); F. InjCase(F; p1. notC(p1); F. InjCase(F; x. x/p2,p3. andC(p2;p3); F. InjCase(F; x. x/p4,p5. orC(p4;p5), x/p6,p7. impC(p6;p7))))) |
|
| fvar | Def 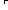 F F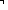 == inl(F) == inl(F) |
| | | Thm*  x:Var. x:Var. 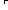 x x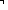 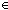 Formula Formula |
|
| nat | Def 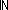 == {i: == {i: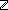 | 0 | 0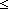 i } i } |
| | | Thm* 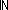 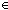 Type Type |
|
| letrec_body | Def = b == b |
|
| letrec_arg | Def x b(x) (x) == b(x) |
|
| letrec | Def (letrec f b(f)) == b((letrec f b(f)) ) (recursive) |
|
| le | Def A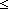 B == B == 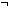 B < A B < A |
| | | Thm*  i,j: i,j: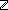 . (i . (i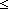 j) j) 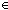 Prop Prop |
|
| not | Def 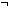 A == A A == A 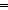 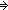 False False |
| | | Thm*  A:Prop. ( A:Prop. (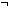 A) A) 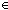 Prop Prop |