Selected Objects
| Introduction | Introductory Remarks |
| THM | eta_conv |
 f:(A f:(A  B). ( B). (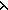 x.f(x)) = f x.f(x)) = f |
| def | tlambda |
(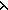 x:T. b(x))(x) == b(x) x:T. b(x))(x) == b(x) |
| def | identity |
Id(x) == x |
| def | tidentity |
Id == Id |
| def | compose |
(f o g)(x) == f(g(x)) |
| THM | comp_assoc |
 f:(A f:(A  B), g:(B B), g:(B  C), h:(C C), h:(C  D). h o (g o f) = (h o g) o f D). h o (g o f) = (h o g) o f 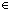 A A  D D |
| THM | comp_id_l |
 f:(A f:(A  B). Id o f = f B). Id o f = f |
| THM | comp_id_r |
 f:(A f:(A  B). f o Id = f B). f o Id = f |
| def | inv_funs |
InvFuns(A; B; f; g) == g o f = Id & f o g = Id |
| THM | sq_stable__inv_funs |
 f:(A f:(A  B), g:(B B), g:(B  A). SqStable(InvFuns(A; B; f; g)) A). SqStable(InvFuns(A; B; f; g)) |
| def | one_one_corr |
A ~~ B == 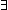 f:(A f:(A  B), g:(B B), g:(B  A). InvFuns(A; B; f; g) A). InvFuns(A; B; f; g) |
| def | inject |
Inj(A; B; f) ==  a1,a2:A. f(a1) = f(a2) a1,a2:A. f(a1) = f(a2) 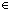 B B 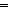 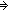 a1 = a2 a1 = a2 |
| def | surject |
Surj(A; B; f) ==  b:B. b:B. 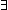 a:A. f(a) = b a:A. f(a) = b |
| def | biject |
Bij(A; B; f) == Inj(A; B; f) & Surj(A; B; f) |
| THM | ax_choice |
 Q:(A Q:(A  B B  Prop). ( Prop). ( x:A. x:A. 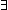 y:B. Q(x,y)) y:B. Q(x,y)) 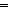 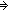 ( (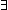 f:(A f:(A  B). B).  x:A. Q(x,f(x))) x:A. Q(x,f(x))) |
| THM | dep_ax_choice |
 B:(A B:(A  Type), Q:(x:A Type), Q:(x:A  B(x) B(x)  Type). Type).
( x:A. x:A. 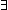 y:B(x). Q(x,y)) y:B(x). Q(x,y)) 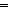 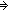 ( (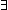 f:(x:A f:(x:A  B(x)). B(x)).  x:A. Q(x,f(x))) x:A. Q(x,f(x))) |
| THM | bij_imp_exists_inv |
 f:(A f:(A  B). Bij(A; B; f) B). Bij(A; B; f) 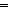 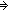 ( (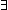 g:(B g:(B  A). InvFuns(A; B; f; g)) A). InvFuns(A; B; f; g)) |
| THM | fun_with_inv_is_bij |
 f:(A f:(A  B), g:(B B), g:(B  A). InvFuns(A; B; f; g) A). InvFuns(A; B; f; g) 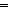 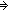 Bij(A; B; f) Bij(A; B; f) |
| THM | bij_iff_1_1_corr |
(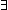 f:(A f:(A  B). Bij(A; B; f)) B). Bij(A; B; f)) 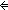 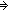 (A ~~ B) (A ~~ B) |