Selected Objects
| def | list_p | T List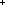 == {l:(T*)| ||l|| > 0 } == {l:(T*)| ||l|| > 0 } |
| def | length_p | ||l|| == ||l|| |
| THM | void_union |  l:Void+T. l l:Void+T. l 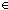 V+T V+T |
| THM | void_union_list |  l:(Void+T)*. l l:(Void+T)*. l 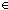 (V+T)* (V+T)* |
| THM | void_union_lang |  L:LangOver(V+T). L L:LangOver(V+T). L 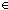 LangOver(Void+T) LangOver(Void+T) |
| def | grammar | Grammar(V;T) == ((V+T List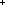 ) )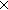 (V+T)*)* (V+T)*)*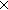 V V |
| def | g_prod | g.prod == 1of(g) |
| def | g_init | g.init == 2of(g) |
| def | produce |  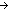 (l1,l2) == (l1,l2) ==  i: i: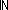 ||G.prod||. < l1,l2 > = G.prod[i] ||G.prod||. < l1,l2 > = G.prod[i] 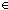 (V+T List (V+T List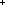 ) )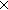 (V+T)* (V+T)* |
| def | directly_derive |  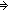 (l,m)
== (l,m)
==  l0:(V+T)*, l1:(V+T List l0:(V+T)*, l1:(V+T List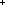 ), l2,m1:(V+T)*. l = (l0 @ l1 @ l2) & (l1 ), l2,m1:(V+T)*. l = (l0 @ l1 @ l2) & (l1  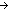 m1) & m = (l0 @ m1 @ l2) m1) & m = (l0 @ m1 @ l2) |
| def | derive |   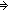 (l,m)
== (l,m)
==  a:((V+T)* List a:((V+T)* List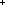 ).
l = a[0] ).
l = a[0] 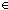 (V+T)* & ( (V+T)* & ( i: i: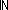 (||a||-1). a[i] (||a||-1). a[i]  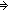 a[(i+1)]) & a[(||a||-1)] = m a[(i+1)]) & a[(||a||-1)] = m 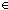 (V+T)* (V+T)* |
| THM | derive_refl |  G:Grammar(V;T), l:(V+T)*. l G:Grammar(V;T), l:(V+T)*. l   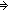 l l |
| THM | derive_trans |  G:Grammar(V;T), l,m,n:(V+T)*. (l G:Grammar(V;T), l,m,n:(V+T)*. (l   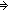 m) m)  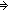 (m (m   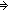 n) n)  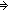 (l (l   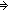 n) n) |
| def | start | S == inl(G.init) |
| def | g_lang | L(G)(l) == [S]   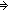 l l |
| def | g_eq | G1 = G2 == L(G1) = L(G2) |
| def | con_sen_g | ConSenG(G) ==  i: i: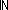 ||G.prod||. ||1of(G.prod[i])|| ||G.prod||. ||1of(G.prod[i])||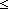 ||2of(G.prod[i])|| ||2of(G.prod[i])|| |
| def | con_free_g | ConFreeG(G)
==  i: i: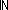 ||G.prod||. ( ||G.prod||. ( a:V. [inl(a)] = 1of(G.prod[i]) a:V. [inl(a)] = 1of(G.prod[i]) 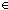 (V+T List (V+T List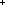 )) & ||2of(G.prod[i])|| > 0 )) & ||2of(G.prod[i])|| > 0 |
| def | reg_g | RegG(G)
==  i: i: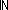 ||G.prod||. ||G.prod||.
 A,B:V, a:T.
G.prod[i] = < [inl(A)],[inr(a); inl(B)] > A,B:V, a:T.
G.prod[i] = < [inl(A)],[inr(a); inl(B)] > 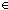 (V+T List (V+T List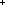 ) )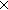 (V+T)* (V+T)*
 G.prod[i] = < [inl(A)],[inr(a)] > G.prod[i] = < [inl(A)],[inr(a)] > 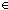 (V+T List (V+T List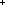 ) )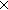 (V+T)* (V+T)* |