is mentioned by

Thm* A,B:T List. no_repeats(T;A) (x:T. (x A) (x B)) (x:T. (x A) & (x B)) ||A|| < ||B||	[length_less]
Thm* A,B:T List. no_repeats(T;A) (x:T. (x A) (x B)) ||A||||B||	[length_le]
Thm* s:T List. no_repeats(T;s) (f:(||s||T). Inj(||s||; T; f))	[no_repeats_inj]
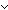Thm* x,z,y,w:T List. ||x|| = ||z|| ||y|| = ||w|| (x @ y) = (z @ w) x = z & y = w	[append_one_one]
Thm* L:Top List, n:{0...||L||}. (firstn(n;L) @ nth_tl(n;L)) ~ L	[append_firstn_lastn_sq]
Thm* s:T List. 0 < ||s|| (s ~ (firstn(||s||-1;s) @ [s[(||s||-1)]]))	[list-decomp-last]
Thm* j:, i:j. ||upto(i;j)|| = j-i	[length_upto]
Thm* x1,z,x2,x3:T List. ||x1|| = ||z|| (x1 @ x2) = (z @ x3) x1 = z & x2 = x3	[equal_appends_eq]
Thm* x1,z,x2,x3:T List. ||z||||x1|| (x1 @ x2) = (z @ x3) (z':T List. x1 = (z @ z') & x3 = (z' @ x2))	[equal_appends_case2]
Thm* x1,z,x2,x3:T List. ||x1||||z|| (x1 @ x2) = (z @ x3) (z':T List. z = (x1 @ z') & x2 = (z' @ x3))	[equal_appends_case1]
Thm* L:T List, P:(T). (xL.P(x)) (i:||L||. P(L[i]))	[assert_l_bexists]
Thm* L:T List, P:(T). (xL.P(x)) (i:||L||. P(L[i]))	[assert_l_ball]

In prior sections: list 1 mb basic mb list 1 mb list 2

Try larger context: Graphs