is mentioned by

Thm* For any graph L:V List, i:V, s:Traversal. (j:V. (inr(j) s) (inl(j) s) j-the_graph- > *i) L-- > *i dfl-traversal(the_graph;L;s) dfl-traversal(the_graph;L;[inr(i) / s])	[dfl-traversal-consr]
Thm* For any graph A:V List, x:V. A-- > *[x] A-- > *x	[list-list-connect-singleton]
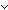Thm* For any graph A,B:V List, i:V. A @ B-- > *i A-- > *i B-- > *i	[list-connect-append]
Thm* For any graph i,j:V. [i]-- > *j i-the_graph- > *j	[list-connect-singleton]
Def dfsl-traversal(the_graph;L;s) == df-traversal(the_graph;s) & (i:Vertices(the_graph). (inl(i) s) L-the_graph- > *i) & ((i:Vertices(the_graph). L-the_graph- > *i non-trivial-loop(the_graph;i)) (L1,L2:Vertices(the_graph) List. L = (L1 @ L2) (s1,s2:traversal(the_graph). s = (s2 @ s1) traversal(the_graph) & paren(Vertices(the_graph);s1) & paren(Vertices(the_graph);s2) & (j:Vertices(the_graph). ((inl(j) s1) L1-the_graph- > *j) & ((inl(j) s2) L2-the_graph- > *j & L1-the_graph- > *j)))))	[dfsl-traversal]
Def dfl-traversal(the_graph;L;s) == (i:Vertices(the_graph), s1,s2:traversal(the_graph). s = (s1 @ [inr(i)] @ s2) traversal(the_graph) (j:Vertices(the_graph). (inr(j) s2) (inl(j) s2) j-the_graph- > *i)) & (j:Vertices(the_graph). (inr(j) s) L-the_graph- > *j) & (i:Vertices(the_graph), s1,s2:traversal(the_graph). (j:Vertices(the_graph). i-the_graph- > *j non-trivial-loop(the_graph;j)) s = (s1 @ [inl(i)] @ s2) traversal(the_graph) L-the_graph- > *i)	[dfl-traversal]
Def L1-G- > *L2 == (xL2.L1-G- > *x)	[list-list-connect]

Try larger context: Graphs