| | Some definitions of interest. |
|
| connect | Def x-the_graph- > *y ==  p:Vertices(the_graph) List. path(the_graph;p) & p[0] = x & last(p) = y p:Vertices(the_graph) List. path(the_graph;p) & p[0] = x & last(p) = y |
| | | Thm* For any graph
 x,y:V. x-the_graph- > *y x,y:V. x-the_graph- > *y  Prop Prop |
|
| decidable | Def Dec(P) == P 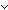  P P |
| | | Thm*  A:Prop. Dec(A) A:Prop. Dec(A)  Prop Prop |
|
| edge | Def x-the_graph- > y ==  e:Edges(the_graph). Incidence(the_graph)(e) = < x,y > e:Edges(the_graph). Incidence(the_graph)(e) = < x,y > |
| | | Thm* For any graph
 x,y:V. x-the_graph- > y x,y:V. x-the_graph- > y  Prop Prop |
|
| gr_v | Def Vertices(t) == 1of(t) |
| | | Thm*  t:Graph. Vertices(t) t:Graph. Vertices(t)  Type Type |
|
| graph | Def Graph == v:Type e:Type e:Type (e (e  v v v) v) Top Top |
| | | Thm* Graph  Type{i'} Type{i'} |
|
| iff | Def P   Q == (P Q == (P   Q) & (P Q) & (P   Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A   B) B)  Prop Prop |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |