Nuprl - Proof: paren induction 2 1

(5steps total) PrintForm Definitions Lemmas graph 1 2 Sections Graphs Doc

At: paren induction 2 1

1. T: Type
2. P: ((T+T) List)Prop
3. P(nil)
4. s1,s2:(T+T) List. P(s1) P(s2) paren(T;s1) paren(T;s2) P(s1 @ s2)
5. s:(T+T) List, t:T. P(s) paren(T;s) P([inl(t)] @ s @ [inr(t)])
6. n:
7. s: (T+T) List
8. s1:(T+T) List. ||s1|| < ||s|| paren(T;s1) P(s1)
9. t: T
10. s': (T+T) List
11. s = ([inl(t)] @ s' @ [inr(t)])
12. paren(T;s')

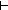||s'|| < ||s||

By: HypSubst -2 0 THEN RWW Thm* as,bs:T List. ||as @ bs|| = ||as||+||bs|| 0 THEN Reduce 0

Generated subgoals:

None

About:

(5steps total) PrintForm Definitions Lemmas graph 1 2 Sections Graphs Doc