Nuprl - Proof: topsortl-properties 1 1

(47steps total) PrintForm Definitions Lemmas graph 1 3 Sections Graphs Doc

1. the_graph: Graph
2. the_obj: GraphObject(the_graph)
3. L: Vertices(the_graph) List
4. i:Vertices(the_graph). (i L)
5. paren(Vertices(the_graph);dfsl(the_obj;L))
6. no_repeats(Vertices(the_graph)+Vertices(the_graph);dfsl(the_obj;L))
7. dfsl-traversal(the_graph;L;dfsl(the_obj;L))
8. i:Vertices(the_graph). (i L) (inr(i) dfsl(the_obj;L)) & (inl(i) dfsl(the_obj;L))
9. non-trivial-loop-free(the_graph)

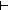
L1,L2:Vertices(the_graph) List. L = (L1 @ L2) (s1,s2:Vertices(the_graph) List. topsortl(the_obj;L) = (s2 @ s1) & (j:Vertices(the_graph). ((j s1) L1-the_graph- > *j) & ((j s2) L2-the_graph- > *j & L1-the_graph- > *j)))

By: let h 7 in (((((Unfold `topsortl` 0) THEN (Unfold `dfsl-traversal` h) THEN (Analyze h) THEN (Analyze h+1)) THENA (Auto THEN (AllHyps (h.(Unfold `non-trivial-loop-free` h) THEN (BackThru h))))) THEN (RepeatFor 3 (ParallelOp -1)) THEN ExRepD THEN (InstConcl [mapoutl(s1);mapoutl(s2)]) THEN (RWO "mapoutl_append < " 0)) THEN (RWO Thm* s:(A+B) List, x:A. (x mapoutl(s)) (inl(x) s) 0)) THEN (Analyze 0) THEN (Try Trivial) THEN Analyze

Generated subgoals:

None

About:

(47steps total) PrintForm Definitions Lemmas graph 1 3 Sections Graphs Doc