| | Some definitions of interest. |
|
| ball | Def   x:T. P(x) == x:T. P(x) == 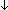  ( ( x:T. x:T. 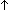 P(x)) P(x)) |
| | | Thm*  T:Type, P:(T T:Type, P:(T   ). ( ). (  x:T. P(x)) x:T. P(x))   |
|
| band | Def p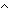 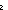 q == if p q == if p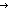 q else false q else false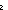 fi fi |
| | | Thm*  p,q: p,q: . (p . (p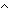 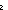 q) q)   |
|
| bequal | Def x = y == y == 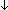  (x = y (x = y  T) T) |
| | | Thm*  T:Type, x,y:T. (x = T:Type, x,y:T. (x = y) y)   |
|
| bexists | Def   x:T. P(x) == x:T. P(x) == 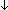  ( ( x:T. x:T. 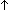 P(x)) P(x)) |
| | | Thm*  T:Type, P:(T T:Type, P:(T   ). ( ). (  x:T. P(x)) x:T. P(x))   |
|
| bimplies | Def p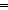  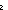 q == q == 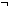 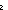 p p 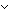 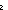 q q |
| | | Thm*  p,q: p,q: . p . p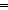  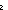 q q   |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A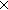 B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |
|
| stype | Def S == {T:Type|  x:T. True } x:T. True } |
| | | Thm* S  Type{2} Type{2} |
|
| tlambda | Def ( x:T. b(x))(x) == b(x) x:T. b(x))(x) == b(x) |