| | Some definitions of interest. |
|
| bequal | Def x = y == y == 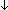  (x = y (x = y  T) T) |
| | | Thm*  T:Type, x,y:T. (x = T:Type, x,y:T. (x = y) y)   |
|
| eq_pred_marker | Def <eq_pred:x> == x |
| | | Thm*  'a:S. <eq_pred:( 'a:S. <eq_pred:(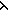 x:'a. x:'a. 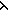 y:'a. x = y:'a. x = y)> y)>  eq('a) eq('a) |
|
| stype | Def S == {T:Type|  x:T. True } x:T. True } |
| | | Thm* S  Type{2} Type{2} |
|
| tlambda | Def (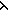 x:T. b(x))(x) == b(x) x:T. b(x))(x) == b(x) |