Selected Objects
| THM | not_exp_0 |
 m,n: m,n: . . 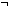 exp(n+1;m) = 0 exp(n+1;m) = 0 |
| THM | zero_less_exp |
 m,n: m,n: . 0<exp(n+1;m) . 0<exp(n+1;m) |
| THM | odd_or_even |
 n: n: . . 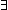 m: m: . n = (0+1+1) . n = (0+1+1)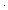 m m    n = (0+1+1) n = (0+1+1) m+1 m+1   |
| THM | less_exp_suc_mono |
 n,m: n,m: . exp(m+1+1;n)<exp(m+1+1;n+1) . exp(m+1+1;n)<exp(m+1+1;n+1) |
| THM | less_less_cases |
 m,n: m,n: . m = n . m = n  m<n m<n 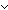 n<m n<m |
| THM | greater_eq |
 n,m: n,m: . True . True |
| THM | less_eq_cases |
 m,n: m,n: . m . m n n 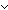 n n m m |
| THM | less_equal_add |
 m,n: m,n: . m . m n n 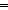  ( (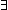 x: x: . n = m+x . n = m+x 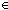  ) ) |
| THM | less_eq_exists |
 m,n: m,n: . m . m n n   ( (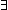 x: x: . n = m+x . n = m+x 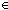  ) ) |
| THM | not_less_equal |
 m,n: m,n: . . 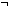 m m n n   n<m n<m |
| THM | less_eq_0 |
 n: n: . n . n 0 0   n = 0 n = 0 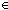  |
| THM | mult_eq_0 |
 m,n: m,n: . m . m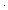 n = 0 n = 0 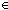    m = 0 m = 0 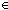  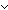 n = 0 n = 0 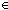  |
| THM | less_mult2 |
 m,n: m,n: . 0<m & 0<n . 0<m & 0<n 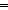  0<m 0<m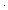 n n |
| THM | less_eq_less_trans |
 m,n,x: m,n,x: . m . m n & n<x n & n<x 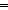  m<x m<x |
| THM | less_less_eq_trans |
 m,n,x: m,n,x: . m<n & n . m<n & n x x 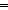  m<x m<x |
| THM | fact_less |
 n: n: . 0<fact(n) . 0<fact(n) |
| THM | even_odd |
 n: n: . even(n) . even(n)   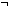 odd(n) odd(n) |
| THM | odd_even |
 n: n: . odd(n) . odd(n)   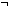 even(n) even(n) |
| THM | even_or_odd |
 n: n: . even(n) . even(n) 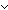 odd(n) odd(n) |
| THM | even_and_odd |
 n: n: . . 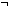 (even(n) & odd(n)) (even(n) & odd(n)) |
| THM | even_add |
 m,n: m,n: . even(m+n) . even(m+n)   (even(m) (even(m)   even(n)) even(n)) |
| THM | even_mult |
 m,n: m,n: . even(m . even(m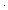 n) n)   even(m) even(m) 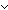 even(n) even(n) |
| THM | odd_add |
 m,n: m,n: . odd(m+n) . odd(m+n)   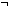 (odd(m) (odd(m)   odd(n)) odd(n)) |
| THM | odd_mult |
 m,n: m,n: . odd(m . odd(m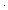 n) n)   odd(m) & odd(n) odd(m) & odd(n) |
| THM | even_double |
 n: n: . even(2 . even(2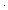 n) n) |
| THM | odd_double |
 n: n: . odd(2 . odd(2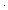 n+1) n+1) |
| THM | even_odd_exists |
 n: n: . (even(n) . (even(n) 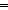  ( (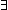 m: m: . n = 2 . n = 2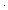 m m 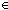  )) & (odd(n) )) & (odd(n) 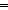  ( (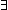 m: m: . n = 2 . n = 2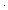 m+1 m+1 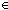  )) )) |
| THM | even_exists |
 n: n: . even(n) . even(n)   ( (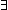 m: m: . n = 2 . n = 2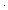 m m 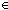  ) ) |
| THM | odd_exists |
 n: n: . odd(n) . odd(n)   ( (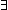 m: m: . n = 2 . n = 2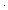 m+1 m+1 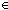  ) ) |
| THM | eq_less_eq |
 m,n: m,n: . m = n . m = n   m m n & n n & n m m |
| THM | add_mono_less_eq |
 m,n,x: m,n,x: . m+n . m+n m+x m+x   n n x x |
| THM | not_suc_less_eq_0 |
 n: n: . . 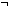 n+1 n+1 0 0 |
| THM | not_leq |
 m,n: m,n: . . 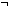 m m n n   n+1 n+1 m m |
| THM | not_num_eq |
 m,n: m,n: . . 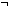 m = n m = n   m+1 m+1 n n 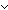 n+1 n+1 m m |
| THM | not_greater |
 m,n: m,n: . . 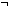 n<m n<m   m m n n |
| THM | not_greater_eq |
 m,n: m,n: . . 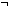 n n m m   m+1 m+1 n n |
| THM | suc_one_add |
 n: n: . n+1 = 1+n . n+1 = 1+n 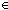  |
| THM | suc_add_sym |
 m,n: m,n: . m+n+1 = n+1+m . m+n+1 = n+1+m 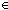  |
| THM | not_suc_add_less_eq |
 m,n: m,n: . . 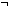 m+n+1 m+n+1 m m |
| THM | mult_less_eq_suc |
 m,n,x: m,n,x: . m . m n n   (x+1) (x+1)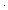 m m (x+1) (x+1)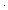 n n |
| THM | sub_left_add |
 m,n,x: m,n,x: . m+nnsub(n;x) = if n . m+nnsub(n;x) = if n 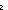 x then m else nnsub(m+n;x) fi x then m else nnsub(m+n;x) fi |
| THM | sub_right_add |
 m,n,x: m,n,x: . nnsub(m;n)+x = if m . nnsub(m;n)+x = if m 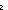 n then x else nnsub(m+x;n) fi n then x else nnsub(m+x;n) fi |
| THM | sub_left_sub |
 m,n,x: m,n,x: . nnsub(m;nnsub(n;x)) = if n . nnsub(m;nnsub(n;x)) = if n 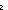 x then m else nnsub(m+x;n) fi x then m else nnsub(m+x;n) fi |
| THM | sub_right_sub |
 m,n,x: m,n,x: . nnsub(nnsub(m;n);x) = nnsub(m;n+x) . nnsub(nnsub(m;n);x) = nnsub(m;n+x) |
| THM | sub_left_suc |
 m,n: m,n: . nnsub(m;n)+1 = if m . nnsub(m;n)+1 = if m 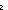 n then 0+1 else nnsub(m+1;n) fi n then 0+1 else nnsub(m+1;n) fi |
| THM | sub_left_less_eq |
 m,n,x: m,n,x: . m . m nnsub(n;x) nnsub(n;x)   m+x m+x n n 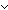 m m 0 0 |
| THM | sub_right_less_eq |
 m,n,x: m,n,x: . nnsub(m;n) . nnsub(m;n) x x   m m n+x n+x |
| THM | sub_left_less |
 m,n,x: m,n,x: . m<nnsub(n;x) . m<nnsub(n;x)   m+x<n m+x<n |
| THM | sub_right_less |
 m,n,x: m,n,x: . nnsub(m;n)<x . nnsub(m;n)<x   m<n+x & 0<x m<n+x & 0<x |
| THM | sub_left_greater_eq |
 m,n,x: m,n,x: . nnsub(n;x) . nnsub(n;x) m m   n n m+x m+x |
| THM | sub_right_greater_eq |
 m,n,x: m,n,x: . x . x nnsub(m;n) nnsub(m;n)   n+x n+x m m 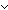 x x 0 0 |
| THM | sub_left_greater |
 m,n,x: m,n,x: . nnsub(n;x)<m . nnsub(n;x)<m   n<m+x & 0<m n<m+x & 0<m |
| THM | sub_right_greater |
 m,n,x: m,n,x: . x<nnsub(m;n) . x<nnsub(m;n)   n+x<m n+x<m |
| THM | sub_left_eq |
 m,n,x: m,n,x: . m = nnsub(n;x) . m = nnsub(n;x)   m+x = n m+x = n 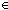  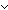 m m 0 & n 0 & n x x |
| THM | sub_right_eq |
 m,n,x: m,n,x: . nnsub(m;n) = x . nnsub(m;n) = x   m = n+x m = n+x 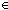  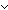 m m n & x n & x 0 0 |