Def (x:T. b(x))(x) == b(x)

is mentioned by

Thm* exists(f:hind  hind. and(one_one(f),not(onto(f))))	[hinfinity_ax]
Thm* 'a:S. all(P:'a  hbool. all(x:'a. implies(P(x),P(select(P)))))	[hselect_ax]
Thm* 'b,'a:S. all(t:'a  'b. equal((x:'a. t(x)),t))	[heta_ax]
Thm* all Thm* (t1:hbool. all Thm* (t1:hbool. (t2:hbool. implies Thm* (t1:hbool. (t2:hbool. (implies(t1,t2) Thm* (t1:hbool. (t2:hbool. ,implies(implies(t2,t1),equal(t1,t2)))))	[himp_antisym_ax]
Thm* all(t:hbool. or(equal(t,t),equal(t,f)))	[hbool_cases_ax]
Thm* 'b,'a:S. Thm* all Thm* (P:'a  hbool. all Thm* (P:'a  hbool. (rep:'b  'a. equal Thm* (P:'a  hbool. (rep:'b  'a. (type_definition(P,rep) Thm* (P:'a  hbool. (rep:'b  'a. ,and Thm* (P:'a  hbool. (rep:'b  'a. ,(all Thm* (P:'a  hbool. (rep:'b  'a. ,((x':'b. all Thm* (P:'a  hbool. (rep:'b  'a. ,((x':'b. (x'':'b. implies Thm* (P:'a  hbool. (rep:'b  'a. ,((x':'b. (x'':'b. (equal Thm* (P:'a  hbool. (rep:'b  'a. ,((x':'b. (x'':'b. ((rep(x') Thm* (P:'a  hbool. (rep:'b  'a. ,((x':'b. (x'':'b. (,rep(x'')) Thm* (P:'a  hbool. (rep:'b  'a. ,((x':'b. (x'':'b. ,equal(x',x'')))) Thm* (P:'a  hbool. (rep:'b  'a. ,,all Thm* (P:'a  hbool. (rep:'b  'a. ,,(x:'a. equal Thm* (P:'a  hbool. (rep:'b  'a. ,,(x:'a. (P(x) Thm* (P:'a  hbool. (rep:'b  'a. ,,(x:'a. ,exists Thm* (P:'a  hbool. (rep:'b  'a. ,,(x:'a. ,(x':'b. equal Thm* (P:'a  hbool. (rep:'b  'a. ,,(x:'a. ,(x':'b. (x Thm* (P:'a  hbool. (rep:'b  'a. ,,(x:'a. ,(x':'b. ,rep(x')))))))))	[htype_definition_wd]
Thm* 'a,'b:S. Thm* all(f:'a  'b. equal(onto(f),all(y:'b. exists(x:'a. equal(y,f(x))))))	[honto_def]
Thm* 'b,'a:S. Thm* all Thm* (f:'a  'b. equal Thm* (f:'a  'b. (one_one(f) Thm* (f:'a  'b. ,all Thm* (f:'a  'b. ,(x1:'a. all Thm* (f:'a  'b. ,(x1:'a. (x2:'a. implies Thm* (f:'a  'b. ,(x1:'a. (x2:'a. (equal(f(x1),f(x2)) Thm* (f:'a  'b. ,(x1:'a. (x2:'a. ,equal(x1,x2))))))	[hone_one_def]
Thm* 'a:S.  Thm* equal Thm* (cond Thm* ,t:hbool. t1:'a. t2:'a. select Thm* ,t:hbool. t1:'a. t2:'a. (x:'a. and Thm* ,t:hbool. t1:'a. t2:'a. (x:'a. (implies(equal(t,t),equal(x,t1)) Thm* ,t:hbool. t1:'a. t2:'a. (x:'a. ,implies(equal(t,f),equal(x,t2)))))	[hcond_def]
Thm* 'b,'a:S. equal(let,f:'a  'b. x:'a. f(x))	[hlet_def]
Thm* 'a:S.  Thm* equal Thm* (exists_unique Thm* ,P:'a  hbool. and Thm* ,P:'a  hbool. (exists(P) Thm* ,P:'a  hbool. ,all Thm* ,P:'a  hbool. ,(x:'a. all(y:'a. implies(and(P(x),P(y)),equal(x,y))))))	[hexists_unique_def]
Thm* equal(not,t:hbool. implies(t,f))	[hnot_def]
Thm* equal(f,all(t:hbool. t))	[hf_def]
Thm* equal Thm* (or Thm* ,t1:hbool. t2:hbool. all Thm* ,t1:hbool. t2:hbool. (t:hbool. implies Thm* ,t1:hbool. t2:hbool. (t:hbool. (implies(t1,t) Thm* ,t1:hbool. t2:hbool. (t:hbool. ,implies(implies(t2,t),t))))	[hor_def]
Thm* equal Thm* (and Thm* ,t1:hbool. t2:hbool. all(t:hbool. implies(implies(t1,implies(t2,t)),t)))	[hand_def]
Thm* 'a:S. equal(all,P:'a  hbool. equal(P,x:'a. t))	[hforall_def]
Thm* equal(t,equal((x:hbool. x),x:hbool. x))	[htruth]
Thm* 'a:S. equal(exists,P:'a  hbool. P(select(P)))	[hexists_def]
Def type_definition == P:'a. 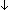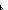rep:'b'a. type_definition('a;'b;P;rep)	[htype_definition]
Def onto == f:'a'b. 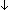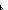onto('a;'b;f)	[honto]
Def one_one == f:'a'b. 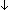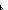one_one('a;'b;f)	[hone_one]
Def cond == b:. p:'a. q:'a. if b then p else q fi	[hcond]
Def let == f:'a'b. e:'a. let x = e in f(x)	[hlet]
Def exists_unique == p:'a. b_exists_unique('a;x.p(x))	[hexists_unique]
Def not 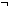== p:. p	[hnot]
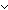Def or == p:. q:. p  q	[hor]
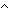Def and == p:. q:. pq	[hand]
Def all == p:'a. 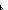x:'a. (p(x))	[hall]
Def exists == p:'a. 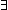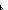x:'a. (p(x))	[hexists]

In prior sections: hol hol min

Try larger context: HOLlib IF YOU CAN SEE THIS go to /sfa/Nuprl/Shared/Xindentation_hack_doc.html