Thm* all( m:hnum. equal(suc(m),abs_num(suc_rep(rep_num(m))))) m:hnum. equal(suc(m),abs_num(suc_rep(rep_num(m))))) | [hsuc_def] |
Thm* all
Thm* ( m:hind. equal m:hind. equal
Thm* ( m:hind. (is_num_rep(m) m:hind. (is_num_rep(m)
Thm* ( m:hind. ,all m:hind. ,all
Thm* ( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. implies hbool. implies
Thm* ( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. (and hbool. (and
Thm* ( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. ((P(zero_rep) hbool. ((P(zero_rep)
Thm* ( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. (,all( hbool. (,all( n:hind. implies(P(n),P(suc_rep(n))))) n:hind. implies(P(n),P(suc_rep(n)))))
Thm* ( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. ,P(m))))) hbool. ,P(m))))) | [his_num_rep_wd] |
Thm* equal(zero_rep,select( x:hind. all( x:hind. all( y:hind. not(equal(x,suc_rep(y)))))) y:hind. not(equal(x,suc_rep(y)))))) | [hzero_rep_def] |
Thm* equal(suc_rep,select( f:hind f:hind   hind. and(one_one(f),not(onto(f))))) hind. and(one_one(f),not(onto(f))))) | [hsuc_rep_def] |
Def rep_num ==  n: n: . ncompose(suc_rep;n;zero_rep) . ncompose(suc_rep;n;zero_rep) | [hrep_num] |
Def is_num_rep
Def ==  m: m: . .  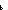 P: P:   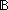
Def ==  m: m: . .   ((P(zero_rep)) ((P(zero_rep))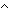 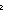 ( ( 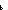 n: n: . (P(n)) . (P(n))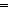 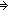 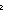 (P(suc_rep(n))))) (P(suc_rep(n)))))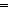 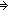 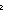 (P(m)) (P(m)) | [his_num_rep] |
Def zero_rep == @x: . ( . ( y: y: . . 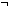 x = suc_rep(y) x = suc_rep(y)   ) ) | [hzero_rep] |