Selected Objects
| def | ncompose |
ncompose(f;n;x) == if n=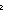 0 then x else f(ncompose(f;n-1;x)) fi (recursive) 0 then x else f(ncompose(f;n-1;x)) fi (recursive) |
| THM | ncompose_zero |
 f:('a f:('a  'a), x:'a. ncompose(f;0;x) = x 'a), x:'a. ncompose(f;0;x) = x |
| THM | ncompose_pos |
 n: n: , x:'a, f:('a , x:'a, f:('a  'a). n>0 'a). n>0 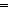  ncompose(f;n;x) = f(ncompose(f;n-1;x)) ncompose(f;n;x) = f(ncompose(f;n-1;x)) |
| THM | decidable__nat |
 m,n: m,n: . Dec(m = n) . Dec(m = n) |
| THM | nat_eq_to_int |
 m,n: m,n: . m = n . m = n 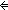 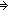 m = n m = n |
| def | hnum |
hnum ==  |
| def | hsuc_rep |
suc_rep ==  x: x: . (@f: . (@f:    . (one_one( . (one_one( ; ; ;f) & ;f) & 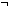 onto( onto( ; ; ;f)))(x) ;f)))(x) |
| def | hzero_rep |
zero_rep == @x: . ( . ( y: y: . . 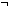 x = suc_rep(y) x = suc_rep(y)   ) ) |
| def | his_num_rep |
is_num_rep
==  m: m: . .  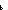 P: P:   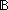 . ((P(zero_rep)) . ((P(zero_rep))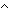 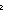 ( ( 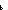 n: n: . (P(n)) . (P(n))   (P(suc_rep(n))))) (P(suc_rep(n))))) 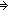 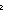 (P(m)) (P(m)) |
| def | hrep_num |
rep_num ==  n: n: . ncompose(suc_rep;n;zero_rep) . ncompose(suc_rep;n;zero_rep) |
| def | habs_num |
abs_num ==  n: n: . @m: . @m: . (n = rep_num(m) . (n = rep_num(m)   ) ) |
| def | hzero |
zero == 0 |
| def | hsuc |
suc ==  n: n: . n+1 . n+1 |
| THM | num_iso |
iso_pair( ; ; ;is_num_rep;rep_num;abs_num) ;is_num_rep;rep_num;abs_num) |
| THM | hsuc_rep_def |
equal(suc_rep,select( f:hind f:hind   hind. and(one_one(f),not(onto(f))))) hind. and(one_one(f),not(onto(f))))) |
| THM | hzero_rep_def |
equal(zero_rep,select( x:hind. all( x:hind. all( y:hind. not(equal(x,suc_rep(y)))))) y:hind. not(equal(x,suc_rep(y)))))) |
| THM | his_num_rep_wd |
all
( m:hind. equal m:hind. equal
( m:hind. (is_num_rep(m) m:hind. (is_num_rep(m)
( m:hind. ,all m:hind. ,all
( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. implies hbool. implies
( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. (and hbool. (and
( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. ((P(zero_rep) hbool. ((P(zero_rep)
( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. (,all( hbool. (,all( n:hind. implies(P(n),P(suc_rep(n))))) n:hind. implies(P(n),P(suc_rep(n)))))
( m:hind. ,( m:hind. ,( P:hind P:hind   hbool. ,P(m))))) hbool. ,P(m))))) |
| THM | hnum_ty_def |
exists( rep:hnum rep:hnum   hind. type_definition(is_num_rep,rep)) hind. type_definition(is_num_rep,rep)) |
| THM | hnum_iso_def |
and
(all( a:hnum. equal(abs_num(rep_num(a)),a)) a:hnum. equal(abs_num(rep_num(a)),a))
,all( r:hind. equal(is_num_rep(r),equal(rep_num(abs_num(r)),r)))) r:hind. equal(is_num_rep(r),equal(rep_num(abs_num(r)),r)))) |
| THM | hzero_def |
equal(0,abs_num(zero_rep)) |
| THM | hsuc_def |
all( m:hnum. equal(suc(m),abs_num(suc_rep(rep_num(m))))) m:hnum. equal(suc(m),abs_num(suc_rep(rep_num(m))))) |
| THM | hnot_suc |
all( n:hnum. not(equal(suc(n),0))) n:hnum. not(equal(suc(n),0))) |
| THM | hinv_suc |
all( m:hnum. all( m:hnum. all( n:hnum. implies(equal(suc(m),suc(n)),equal(m,n)))) n:hnum. implies(equal(suc(m),suc(n)),equal(m,n)))) |
| THM | hinduction |
all
( P:hnum P:hnum   hbool. implies hbool. implies
( P:hnum P:hnum   hbool. (and(P(0),all( hbool. (and(P(0),all( n:hnum. implies(P(n),P(suc(n))))) n:hnum. implies(P(n),P(suc(n)))))
( P:hnum P:hnum   hbool. ,all( hbool. ,all( n:hnum. P(n)))) n:hnum. P(n)))) |
| THM | not_suc |
 n: n: . . 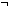 n+1 = 0 n+1 = 0   |
| THM | inv_suc |
 m,n: m,n: . m+1 = n+1 . m+1 = n+1   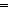 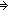 m = n m = n |
| THM | induction |
 P:( P:(   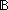 ). P(0) & ( ). P(0) & ( n: n: . P(n) . P(n) 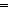 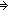 P(n+1)) P(n+1))   ( ( n: n: . P(n)) . P(n)) |