Selected Objects
| def | hprod |
hprod('a; 'b) == 'a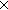 'b 'b |
| def | hmk_pair |
mk_pair ==  x:'a. x:'a.  y:'b. y:'b.  a:'a. a:'a.  b:'b. (a = b:'b. (a =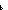 x) x)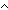 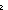 (b = (b =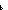 y) y) |
| def | his_pair |
is_pair ==  p:'a p:'a  'b 'b  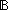 . . 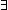 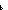 x:'a. x:'a. 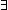 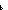 y:'b. (p = y:'b. (p =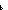 (mk_pair(x,y))) (mk_pair(x,y))) |
| def | hrep_prod |
rep_prod ==  p:'a p:'a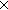 'b. mk_pair(1of(p),2of(p)) 'b. mk_pair(1of(p),2of(p)) |
| def | hpair |
pair ==  x:'a. x:'a.  y:'b. <x,y> y:'b. <x,y> |
| def | hfst |
fst ==  p:'a p:'a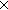 'b. 1of(p) 'b. 1of(p) |
| def | hsnd |
snd ==  p:'a p:'a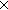 'b. 2of(p) 'b. 2of(p) |
| def | huncurry |
uncurry ==  f:'a f:'a  'b 'b  'c. 'c.  p:'a p:'a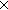 'b. f(1of(p),2of(p)) 'b. f(1of(p),2of(p)) |
| def | hcurry |
curry ==  f:'a f:'a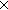 'b 'b  'c. 'c.  x:'a. x:'a.  y:'b. f(<x,y>) y:'b. f(<x,y>) |
| THM | hmk_pair_def |
 'a,'b:S. 'a,'b:S.
all
( x:'a. all x:'a. all
( x:'a. ( x:'a. ( y:'b. equal(mk_pair(x,y), y:'b. equal(mk_pair(x,y), a:'a. a:'a.  b:'b. and(equal(a,x),equal(b,y))))) b:'b. and(equal(a,x),equal(b,y))))) |
| THM | his_pair_def |
 'a,'b:S. 'a,'b:S.
all
( p:'a p:'a   'b 'b   hbool. equal hbool. equal
( p:'a p:'a   'b 'b   hbool. (is_pair(p) hbool. (is_pair(p)
( p:'a p:'a   'b 'b   hbool. ,exists( hbool. ,exists( x:'a. exists( x:'a. exists( y:'b. equal(p,mk_pair(x,y)))))) y:'b. equal(p,mk_pair(x,y)))))) |
| THM | hrep_prod_wd |
 'a,'b:S. 'a,'b:S.
equal
(rep_prod
,select
,( rep:hprod('a; 'b) rep:hprod('a; 'b)
,(  'a 'a
,(  'b 'b
,(  hbool. and hbool. and
,(  hbool. (all hbool. (all
,(  hbool. (( hbool. (( p':hprod('a; 'b). all p':hprod('a; 'b). all
,(  hbool. (( hbool. (( p':hprod('a; 'b). ( p':hprod('a; 'b). ( p'':hprod('a; 'b). implies p'':hprod('a; 'b). implies
,(  hbool. (( hbool. (( p':hprod('a; 'b). ( p':hprod('a; 'b). ( p'':hprod('a; 'b). (equal(rep(p'),rep(p'')) p'':hprod('a; 'b). (equal(rep(p'),rep(p''))
,(  hbool. (( hbool. (( p':hprod('a; 'b). ( p':hprod('a; 'b). ( p'':hprod('a; 'b). ,equal(p',p'')))) p'':hprod('a; 'b). ,equal(p',p''))))
,(  hbool. ,all hbool. ,all
,(  hbool. ,( hbool. ,( p:'a p:'a   'b 'b   hbool. equal hbool. equal
,(  hbool. ,( hbool. ,( p:'a p:'a   'b 'b   hbool. (is_pair(p) hbool. (is_pair(p)
,(  hbool. ,( hbool. ,( p:'a p:'a   'b 'b   hbool. ,exists hbool. ,exists
,(  hbool. ,( hbool. ,( p:'a p:'a   'b 'b   hbool. ,( hbool. ,( p':hprod('a; 'b). equal(p,rep(p')))))))) p':hprod('a; 'b). equal(p,rep(p')))))))) |
| THM | hprod_ty_def |
 'a,'b:S. 'a,'b:S.
exists( rep:hprod('a; 'b) rep:hprod('a; 'b)   'a 'a   'b 'b   hbool. type_definition(is_pair,rep)) hbool. type_definition(is_pair,rep)) |
| THM | hcomma_def |
 'a,'b:S. 'a,'b:S.
all
( x:'a. all x:'a. all
( x:'a. ( x:'a. ( y:'b. equal y:'b. equal
( x:'a. ( x:'a. ( y:'b. (pair(x,y) y:'b. (pair(x,y)
( x:'a. ( x:'a. ( y:'b. ,select( y:'b. ,select( p:hprod('a; 'b). equal(rep_prod(p),mk_pair(x,y)))))) p:hprod('a; 'b). equal(rep_prod(p),mk_pair(x,y)))))) |
| THM | hfst_def |
 'a,'b:S. 'a,'b:S.
all
( p:hprod('a; 'b). equal p:hprod('a; 'b). equal
( p:hprod('a; 'b). (fst(p) p:hprod('a; 'b). (fst(p)
( p:hprod('a; 'b). ,select p:hprod('a; 'b). ,select
( p:hprod('a; 'b). ,( p:hprod('a; 'b). ,( x:'a. exists( x:'a. exists( y:'b. equal(mk_pair(x,y),rep_prod(p)))))) y:'b. equal(mk_pair(x,y),rep_prod(p)))))) |
| THM | hsnd_def |
 'a,'b:S. 'a,'b:S.
all
( p:hprod('a; 'b). equal p:hprod('a; 'b). equal
( p:hprod('a; 'b). (snd(p) p:hprod('a; 'b). (snd(p)
( p:hprod('a; 'b). ,select p:hprod('a; 'b). ,select
( p:hprod('a; 'b). ,( p:hprod('a; 'b). ,( y:'b. exists( y:'b. exists( x:'a. equal(mk_pair(x,y),rep_prod(p)))))) x:'a. equal(mk_pair(x,y),rep_prod(p)))))) |
| THM | huncurry_def |
 'c,'a,'b:S. 'c,'a,'b:S.
all
( f:'a f:'a   'b 'b   'c. all( 'c. all( x:'a. all( x:'a. all( y:'b. equal(uncurry(f,pair(x,y)),f(x,y))))) y:'b. equal(uncurry(f,pair(x,y)),f(x,y))))) |
| THM | hcurry_def |
 'c,'a,'b:S. 'c,'a,'b:S.
all
( f:hprod('a; 'b) f:hprod('a; 'b)   'c. all 'c. all
( f:hprod('a; 'b) f:hprod('a; 'b)   'c. ( 'c. ( x:'a. all( x:'a. all( y:'b. equal(curry(f,x,y),f(pair(x,y)))))) y:'b. equal(curry(f,x,y),f(pair(x,y)))))) |
| THM | hpair_wd |
 'a,'b:S. all( 'a,'b:S. all( x:hprod('a; 'b). equal(pair(fst(x),snd(x)),x)) x:hprod('a; 'b). equal(pair(fst(x),snd(x)),x)) |
| THM | hfst_pair |
 'a,'b:S. all( 'a,'b:S. all( x:'a. all( x:'a. all( y:'b. equal(fst(pair(x,y)),x))) y:'b. equal(fst(pair(x,y)),x))) |
| THM | hsnd_pair |
 'a,'b:S. all( 'a,'b:S. all( x:'a. all( x:'a. all( y:'b. equal(snd(pair(x,y)),y))) y:'b. equal(snd(pair(x,y)),y))) |
| THM | hpair_eq |
 'a,'b:S. 'a,'b:S.
all
( b:'b. all b:'b. all
( b:'b. ( b:'b. ( a:'a. all a:'a. all
( b:'b. ( b:'b. ( a:'a. ( a:'a. ( y:'b. all y:'b. all
( b:'b. ( b:'b. ( a:'a. ( a:'a. ( y:'b. ( y:'b. ( x:'a. equal x:'a. equal
( b:'b. ( b:'b. ( a:'a. ( a:'a. ( y:'b. ( y:'b. ( x:'a. (equal(pair(x,y),pair(a,b)) x:'a. (equal(pair(x,y),pair(a,b))
( b:'b. ( b:'b. ( a:'a. ( a:'a. ( y:'b. ( y:'b. ( x:'a. ,and(equal(x,a),equal(y,b))))))) x:'a. ,and(equal(x,a),equal(y,b))))))) |
| THM | pair_wd |
 'a,'b:S, x:('a 'a,'b:S, x:('a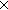 'b). <1of(x),2of(x)> = x 'b). <1of(x),2of(x)> = x |
| THM | fst_pair |
 'a,'b:S, x:'a, y:'b. x = x 'a,'b:S, x:'a, y:'b. x = x |
| THM | snd_pair |
 'a,'b:S, x:'a, y:'b. y = y 'a,'b:S, x:'a, y:'b. y = y |
| THM | pair_eq |
 'a,'b:S, b:'b, a:'a, y:'b, x:'a. <x,y> = <a,b> 'a,'b:S, b:'b, a:'a, y:'b, x:'a. <x,y> = <a,b> 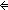 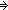 x = a & y = b x = a & y = b |
| THM | pair_unfold |
 'a,'b:S, p:('a 'a,'b:S, p:('a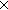 'b). p = <1of(p),2of(p)> 'b). p = <1of(p),2of(p)> |