Thm*  'a,'b:S, u,v:'a+'b. rep_sum(u) = rep_sum(v) 'a,'b:S, u,v:'a+'b. rep_sum(u) = rep_sum(v)     'a 'a  'b 'b   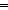 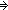 u = v u = v | [hrep_sum_inj] |
Thm*  'a,'b:S. 'a,'b:S.
Thm* ( x:'a+'b. abs_sum(rep_sum(x)) = x x:'a+'b. abs_sum(rep_sum(x)) = x  'a+'b) 'a+'b)
Thm* & ( x:( x:(   'a 'a  'b 'b   ). is_sum_rep(x) = ((rep_sum(abs_sum(x))) = ). is_sum_rep(x) = ((rep_sum(abs_sum(x))) =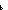 x)) x)) | [sum_iso] |
Thm*  'a,'b:S. 'a,'b:S.
Thm* and
Thm* (all( a:hsum('a; 'b). equal(abs_sum(rep_sum(a)),a)) a:hsum('a; 'b). equal(abs_sum(rep_sum(a)),a))
Thm* ,all
Thm* ,( r:hbool r:hbool   'a 'a   'b 'b   hbool. equal hbool. equal
Thm* ,( r:hbool r:hbool   'a 'a   'b 'b   hbool. (is_sum_rep(r) hbool. (is_sum_rep(r)
Thm* ,( r:hbool r:hbool   'a 'a   'b 'b   hbool. ,equal(rep_sum(abs_sum(r)),r)))) hbool. ,equal(rep_sum(abs_sum(r)),r)))) | [hsum_iso_def] |
Def is_sum_rep ==  f: f:   'a 'a  'b 'b   . . 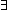 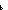 u:'a+'b. (f = u:'a+'b. (f =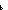 (rep_sum(u))) (rep_sum(u))) | [his_sum_rep] |
Def abs_sum ==  f: f:   'a 'a  'b 'b   . @u:'a+'b. (rep_sum(u) = f . @u:'a+'b. (rep_sum(u) = f     'a 'a  'b 'b   ) ) | [habs_sum] |