Selected Objects
| def | hsum |
hsum('a; 'b) == 'a+'b |
| def | hrep_sum |
rep_sum
==  u:'a+'b. InjCase(u u:'a+'b. InjCase(u
==  u:'a+'b. InjCase; p. u:'a+'b. InjCase; p.  b: b: . .  x:'a. x:'a.  y:'b. (x = y:'b. (x =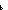 p) p)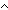 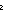 b b
==  u:'a+'b. InjCase; q. u:'a+'b. InjCase; q.  b: b: . .  x:'a. x:'a.  y:'b. (y = y:'b. (y =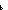 q) q)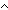 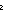 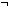 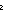 b) b) |
| def | habs_sum |
abs_sum ==  f: f:   'a 'a  'b 'b   . @u:'a+'b. (rep_sum(u) = f . @u:'a+'b. (rep_sum(u) = f     'a 'a  'b 'b   ) ) |
| def | his_sum_rep |
is_sum_rep ==  f: f:   'a 'a  'b 'b   . . 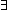 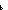 u:'a+'b. (f = u:'a+'b. (f =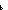 (rep_sum(u))) (rep_sum(u))) |
| def | hinl |
inl ==  x:'a. inl(x) x:'a. inl(x) |
| def | hinr |
inr ==  x:'b. inr(x) x:'b. inr(x) |
| def | hisl |
isl ==  u:'a+'b. isl(u) u:'a+'b. isl(u) |
| def | hisr |
isr ==  u:'a+'b. isr(u) u:'a+'b. isr(u) |
| def | houtl |
outl ==  u:'a+'b. InjCase(u; x. x, arb('a)) u:'a+'b. InjCase(u; x. x, arb('a)) |
| THM | houtl_nuprl |
 'a,'b:S, u:'a+'b. isl(u) 'a,'b:S, u:'a+'b. isl(u) 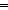 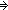 outl(u) = outl(u) outl(u) = outl(u) |
| def | houtr |
outr ==  u:'a+'b. InjCase(u; x. arb('b), x) u:'a+'b. InjCase(u; x. arb('b), x) |
| THM | houtr_nuprl |
 'a,'b:S, u:'a+'b. isr(u) 'a,'b:S, u:'a+'b. isr(u) 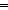 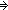 outr(u) = outr(u) outr(u) = outr(u) |
| THM | his_sum_rep_wd |
 'a,'b:S. 'a,'b:S.
all
( f:hbool f:hbool
(  'a 'a
(  'b 'b
(  hbool. equal hbool. equal
(  hbool. (is_sum_rep(f) hbool. (is_sum_rep(f)
(  hbool. ,exists hbool. ,exists
(  hbool. ,( hbool. ,( v1:'a. exists v1:'a. exists
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. or v2:'b. or
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. (equal v2:'b. (equal
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. ((f v2:'b. ((f
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. (, v2:'b. (, b:hbool. b:hbool.  x:'a. x:'a.  y:'b. and(equal(x,v1),b)) y:'b. and(equal(x,v1),b))
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. ,equal v2:'b. ,equal
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. ,(f v2:'b. ,(f
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. ,, v2:'b. ,, b:hbool. b:hbool.  x:'a. x:'a.  y:'b. and y:'b. and
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. ,, v2:'b. ,, b:hbool. b:hbool.  x:'a. x:'a.  y:'b. (equal(y,v2) y:'b. (equal(y,v2)
(  hbool. ,( hbool. ,( v1:'a. ( v1:'a. ( v2:'b. ,, v2:'b. ,, b:hbool. b:hbool.  x:'a. x:'a.  y:'b. ,not(b)))))))) y:'b. ,not(b)))))))) |
| THM | hsum_iso_def |
 'a,'b:S. 'a,'b:S.
and
(all( a:hsum('a; 'b). equal(abs_sum(rep_sum(a)),a)) a:hsum('a; 'b). equal(abs_sum(rep_sum(a)),a))
,all
,( r:hbool r:hbool   'a 'a   'b 'b   hbool. equal hbool. equal
,( r:hbool r:hbool   'a 'a   'b 'b   hbool. (is_sum_rep(r) hbool. (is_sum_rep(r)
,( r:hbool r:hbool   'a 'a   'b 'b   hbool. ,equal(rep_sum(abs_sum(r)),r)))) hbool. ,equal(rep_sum(abs_sum(r)),r)))) |
| THM | sum_iso |
 'a,'b:S. 'a,'b:S.
( x:'a+'b. abs_sum(rep_sum(x)) = x x:'a+'b. abs_sum(rep_sum(x)) = x  'a+'b) 'a+'b)
& ( x:( x:(   'a 'a  'b 'b   ). is_sum_rep(x) = ((rep_sum(abs_sum(x))) = ). is_sum_rep(x) = ((rep_sum(abs_sum(x))) =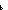 x)) x)) |
| THM | hrep_sum_inj |
 'a,'b:S, u,v:'a+'b. rep_sum(u) = rep_sum(v) 'a,'b:S, u,v:'a+'b. rep_sum(u) = rep_sum(v)     'a 'a  'b 'b   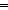 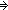 u = v u = v |
| THM | hsum_ty_def |
 'a,'b:S. 'a,'b:S.
exists
( rep:hsum('a; 'b) rep:hsum('a; 'b)   hbool hbool   'a 'a   'b 'b   hbool. type_definition hbool. type_definition
( rep:hsum('a; 'b) rep:hsum('a; 'b)   hbool hbool   'a 'a   'b 'b   hbool. (is_sum_rep hbool. (is_sum_rep
( rep:hsum('a; 'b) rep:hsum('a; 'b)   hbool hbool   'a 'a   'b 'b   hbool. ,rep)) hbool. ,rep)) |
| THM | hinl_def |
 'b,'a:S. 'b,'a:S.
all( e:'a. equal(inl(e),abs_sum( e:'a. equal(inl(e),abs_sum( b:hbool. b:hbool.  x:'a. x:'a.  y:'b. and(equal(x,e),b)))) y:'b. and(equal(x,e),b)))) |
| THM | hinr_def |
 'a,'b:S. 'a,'b:S.
all
( e:'b. equal(inr(e),abs_sum( e:'b. equal(inr(e),abs_sum( b:hbool. b:hbool.  x:'a. x:'a.  y:'b. and(equal(y,e),not(b))))) y:'b. and(equal(y,e),not(b))))) |
| THM | hisl_wd |
 'b,'a:S. and(all( 'b,'a:S. and(all( x:'a. isl(inl(x))),all( x:'a. isl(inl(x))),all( y:'b. not(isl(inr(y))))) y:'b. not(isl(inr(y))))) |
| THM | hisr_wd |
 'a,'b:S. and(all( 'a,'b:S. and(all( x:'b. isr(inr(x))),all( x:'b. isr(inr(x))),all( y:'a. not(isr(inl(y))))) y:'a. not(isr(inl(y))))) |
| THM | houtl_wd |
 'a,'b:S. all( 'a,'b:S. all( x:'a. equal(outl(inl(x)),x)) x:'a. equal(outl(inl(x)),x)) |
| THM | houtr_wd |
 'b,'a:S. all( 'b,'a:S. all( x:'b. equal(outr(inr(x)),x)) x:'b. equal(outr(inr(x)),x)) |
| THM | hsum_axiom |
 'c,'b,'a:S. 'c,'b,'a:S.
all
( f:'a f:'a   'c. all 'c. all
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. exists_unique 'c. exists_unique
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. and 'c. and
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. (equal(o(h,inl),f) 'c. (equal(o(h,inl),f)
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. ,equal(o(h,inr),g))))) 'c. ,equal(o(h,inr),g))))) |
| THM | hsum_axiom_2 |
 'c,'b,'a:S. 'c,'b,'a:S.
all
( f:'a f:'a   'c. all 'c. all
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. exists_unique 'c. exists_unique
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. and 'c. and
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. (all 'c. (all
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. (( 'c. (( x:'a. equal x:'a. equal
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. (( 'c. (( x:'a. (h(inl(x)) x:'a. (h(inl(x))
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. (( 'c. (( x:'a. ,f(x))) x:'a. ,f(x)))
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. ,all 'c. ,all
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. ,( 'c. ,( x:'b. equal x:'b. equal
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. ,( 'c. ,( x:'b. (h(inr(x)) x:'b. (h(inr(x))
( f:'a f:'a   'c. ( 'c. ( g:'b g:'b   'c. ( 'c. ( h:hsum('a; 'b) h:hsum('a; 'b)   'c. ,( 'c. ,( x:'b. ,g(x))))))) x:'b. ,g(x))))))) |
| THM | hisl_or_isr |
 'a,'b:S. all( 'a,'b:S. all( x:hsum('a; 'b). or(isl(x),isr(x))) x:hsum('a; 'b). or(isl(x),isr(x))) |
| THM | hinl_houtl |
 'a,'b:S. all( 'a,'b:S. all( x:hsum('a; 'b). implies(isl(x),equal(inl(outl(x)),x))) x:hsum('a; 'b). implies(isl(x),equal(inl(outl(x)),x))) |
| THM | hinr_houtr |
 'a,'b:S. all( 'a,'b:S. all( x:hsum('a; 'b). implies(isr(x),equal(inr(outr(x)),x))) x:hsum('a; 'b). implies(isr(x),equal(inr(outr(x)),x))) |
| THM | sum_axiom |
 'c,'b,'a:S, f:('a 'c,'b,'a:S, f:('a  'c), g:('b 'c), g:('b  'c). 'c).
(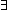 h:(('a+'b) h:(('a+'b)  'c). 'c).
(h o ( x:'a. inl(x)) = f x:'a. inl(x)) = f  'a 'a  'c & h o ( 'c & h o ( x:'b. inr(x)) = g x:'b. inr(x)) = g  'b 'b  'c) 'c)
& ( h,y:(('a+'b) h,y:(('a+'b)  'c). 'c).
& (h o ( x:'a. inl(x)) = f x:'a. inl(x)) = f  'a 'a  'c & h o ( 'c & h o ( x:'b. inr(x)) = g x:'b. inr(x)) = g  'b 'b  'c 'c
& (& y o ( x:'a. inl(x)) = f x:'a. inl(x)) = f  'a 'a  'c 'c
& (& y o ( x:'b. inr(x)) = g x:'b. inr(x)) = g  'b 'b  'c 'c
& (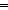 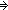
& (h = y) |
| THM | sum_axiom_2 |
 'c,'b,'a:S, f:('a 'c,'b,'a:S, f:('a  'c), g:('b 'c), g:('b  'c). 'c).
(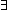 h:(('a+'b) h:(('a+'b)  'c). ( 'c). ( x:'a. h(inl(x)) = f(x)) & ( x:'a. h(inl(x)) = f(x)) & ( x:'b. h(inr(x)) = g(x))) x:'b. h(inr(x)) = g(x)))
& ( h,y:(('a+'b) h,y:(('a+'b)  'c). 'c).
& (( x:'a. h(inl(x)) = f(x)) & ( x:'a. h(inl(x)) = f(x)) & ( x:'b. h(inr(x)) = g(x)) x:'b. h(inr(x)) = g(x))
& (& ( x:'a. y(inl(x)) = f(x)) x:'a. y(inl(x)) = f(x))
& (& ( x:'b. y(inr(x)) = g(x)) x:'b. y(inr(x)) = g(x))
& (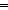 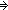
& (h = y) |
| THM | isl_or_isr |
 'a,'b:S, x:'a+'b. isl(x) 'a,'b:S, x:'a+'b. isl(x) 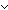 isr(x) isr(x) |
| THM | inl_houtl |
 'a,'b:S, x:'a+'b. isl(x) 'a,'b:S, x:'a+'b. isl(x) 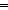 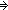 inl(outl(x)) = x inl(outl(x)) = x |
| THM | inr_houtr |
 'a,'b:S, x:'a+'b. isr(x) 'a,'b:S, x:'a+'b. isr(x) 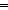  inr(outr(x)) = x inr(outr(x)) = x |