At:
assert term eq
4
2
2
1.
a: Term
2.
u: Term
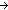Type{i'}
3.
w: a:{v:Term| u(v) }
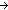
b:Term. term_eq(a;b) 
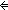
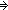a = b
4.
y1: {v:Term| u(v) }
5.
y2: {v:Term| u(v) }
6.
b: Term
7.
u1: Term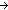Type{i'}
8.
w1: b:{v:Term| u1(v) }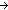term_eq(tree_node( < y1, y2 > );b)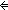 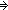tree_node( < y1, y2 > ) = b 
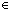Term
9.
y3: {v:Term| u1(v) }
10.
y4: {v:Term| u1(v) }
11.
tree_node( < y1, y2 > ) = tree_node( < y3, y4 > ) 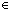Term
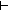y2 = y4
By:
ApFunToHypEquands `z' Case(z) Case u;v = > v Default = > y1 Term -1
THEN
Reduce -1
THEN
TermInd -1
THEN
Reduce 0
Generated subgoals:
None
About:
