Nuprl - Pf closed rel mng 2 1 2 2 2 1 1 1 1 2 1 1

(24steps) PrintForm Definitions Lemmas mb automata 4 Sections GenAutomata Doc

At: closed rel mng 2 1 2 2 2 1 1 1 1 2 1 1

1. r: rel()
2. rho: Decl{i}
3. ds: Collection{i}(dec())
4. daa: Collection{i}(dec())
5. da1: Collection{i}(SimpleType)
6. da2: Collection{i}(SimpleType)
7. de: sig()
8. s: {[[ds]] rho}
9. e: {sig_mng{i:l} (de; rho)}
10. a1: Top
11. a2: Top
12. tr: trace_env([[daa]] rho)
13. trace_consistent_rel(rho;daa;tr.proj;r)
14. tc(r;ds;da1;de)
15. tc(r;ds; < > ;de) & a1 [[ < > ]] rho & a2 [[ < > ]] rho
16. aa: Term List
17. u: Term
18. v: Term List
19. xx:Top. reduce(t,vs. term_free_vars(t) @ vs;nil;v) = nil (list_accum(x,t.x([[t]] 1of(e) s a2 tr);xx;v) ~ list_accum(x,t.x([[t]] 1of(e) s a1 tr);xx;v))
20. xx: Top
21. (term_free_vars(u) @ reduce(t,vs. term_free_vars(t) @ vs;nil;v)) = nil
22. u1: TermType{i'}
23. w: u:{v1:Term| u1(v1) }term_iterate(f.nil;f.nil;f.nil;v.[v];P.nil;x,y. x @ y;u) = nil (iterate(statevar x- > s.x statevar x'- > s.x funsymbol f- > 1of(e).f freevar x- > a2 trace(P)- > tr.P x(y)- > x(y) over u) ~ iterate(statevar x- > s.x statevar x'- > s.x funsymbol f- > 1of(e).f freevar x- > a1 trace(P)- > tr.P x(y)- > x(y) over u))
24. x: Label

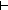[x] = nil (a2 ~ a1)

By: Analyze 0 THEN ApFunToHypEquands `zz' ||zz|| 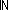-1 THEN Reduce -1

Generated subgoals:

None

About:

(24steps) PrintForm Definitions Lemmas mb automata 4 Sections GenAutomata Doc