Thm*  P:(T P:(T 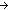 Prop), c1,c2:Collection(T).
c1 = c2 Prop), c1,c2:Collection(T).
c1 = c2 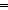  (( (( x x c1.P(x)) c1.P(x)) 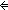  ( ( x x c2.P(x))) c2.P(x))) | [col_all_functionality] |
Thm*  c:Collection(T), P:(T c:Collection(T), P:(T 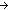 Prop). ( Prop). ( x x c.P(x)) c.P(x)) 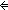  ( ( x:T. x x:T. x  c c 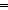  P(x)) P(x)) | [col_all_iff] |
Thm*  l:Collection(T) List, x:T List.
x l:Collection(T) List, x:T List.
x  col_list_prod(l) col_list_prod(l) 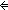  ||x|| = ||l|| ||x|| = ||l||  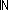 & ( & ( i: i: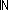 . i < ||x|| . i < ||x|| 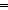  x[i] x[i]  l[i]) l[i]) | [member_col_list_prod] |
Thm*  c:Collection(T), f:(T c:Collection(T), f:(T 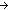 Collection(T')), y:T'.
y Collection(T')), y:T'.
y  ( (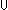 x x c.f(x)) c.f(x)) 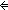  ( (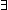 x:T. x x:T. x  c & y c & y  f(x)) f(x)) | [member_col_accum] |
Thm*  a,b:Collection(T), x:T. x a,b:Collection(T), x:T. x  a + b a + b 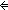  x x  a a 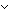 x x  b b | [member_col_add] |
Thm*  c:Collection(T), f:(T c:Collection(T), f:(T 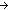 T'), x:T'.
x T'), x:T'.
x  < f(y) | y < f(y) | y  c > c > 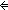  ( (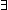 y:T. y y:T. y  c & x = f(y)) c & x = f(y)) | [member_col_map] |
Thm*  C:(I C:(I 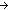 Collection(T)), x:T. x Collection(T)), x:T. x  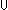 i:I. C(i) i:I. C(i) 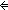  ( (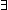 i:I. x i:I. x  C(i)) C(i)) | [member_col_union] |
Thm*  c1:Collection(T). c1 c1:Collection(T). c1 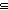 c1 c1 | [col_le_reflexive] |
Thm*  f:(T f:(T 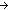 Prop), c:Collection(T), x:T. x Prop), c:Collection(T), x:T. x  < i < i  c | f(i) > c | f(i) > 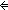  x x  c & f(x) c & f(x) | [member_col_filter] |
Thm*  a1,b1,a2,b2:Collection(T).
a1 = b1 a1,b1,a2,b2:Collection(T).
a1 = b1 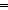  a2 = b2 a2 = b2 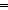  (a1 = a2 (a1 = a2 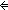  b1 = b2) b1 = b2) | [col_equal_functionality] |
Thm*  a,b,c:Collection(T). a a,b,c:Collection(T). a 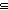 b b 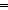  b b 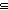 c c 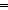  a a 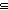 c c | [col_le_transitivity] |
Thm*  c1,c2:Collection(T). c1 = c2 c1,c2:Collection(T). c1 = c2 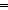  c1 c1 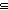 c2 c2 | [col_le_weakening] |
Thm*  c:Collection(T). < > c:Collection(T). < > 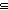 c c | [col_none_le] |
Thm*  c1,c2:Collection(T), t1,t2:T.
t1 = t2 c1,c2:Collection(T), t1,t2:T.
t1 = t2 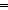  c1 = c2 c1 = c2 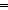  (t1 (t1  c1 c1 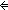  t2 t2  c2) c2) | [col_member_functionality] |
Thm*  c1,c2,c3:Collection(T). c1 = c2 c1,c2,c3:Collection(T). c1 = c2 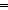  c2 = c3 c2 = c3 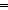  c1 = c3 c1 = c3 | [col_equal_transitivity] |
Thm*  c1,c2:Collection(T). c1 = c2 c1,c2:Collection(T). c1 = c2 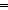  c2 = c1 c2 = c1 | [col_equal_inversion] |
Thm*  c1,c2:Collection(T). c1 = c2 c1,c2:Collection(T). c1 = c2 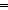  c1 = c2 c1 = c2 | [col_equal_weakening] |
Thm*  T:Type{i'}, x:T. x T:Type{i'}, x:T. x  < > < > 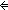  False False | [member_col_none] |
Def ( x x c.P(x)) == c.P(x)) ==  x:T. x x:T. x  c c 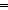  P(x) P(x) | [col_all] |
Def col_list_prod(l)(x) == ||x|| = ||l||  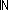 & ( & ( i: i: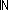 . i < ||x|| . i < ||x|| 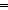  x[i] x[i]  l[i]) l[i]) | [col_list_prod] |
Def c1 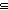 c2 == c2 ==  x:T. x x:T. x  c1 c1 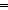  x x  c2 c2 | [col_le] |
Def c1 = c2 ==  x:T. x x:T. x  c1 c1 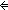  x x  c2 c2 | [col_equal] |