| | Some definitions of interest. |
|
| ESAxioms | Def ESAxioms{i:l}
Def ESAxioms(E;
Def ESAxioms(T;
Def ESAxioms(M;
Def ESAxioms(loc;
Def ESAxioms(kind;
Def ESAxioms(val;
Def ESAxioms(when;
Def ESAxioms(after;
Def ESAxioms(sends;
Def ESAxioms(sender;
Def ESAxioms(index;
Def ESAxioms(first;
Def ESAxioms(pred;
Def ESAxioms(causl)
Def == ( e,e':E. loc(e) = loc(e') e,e':E. loc(e) = loc(e')  Id Id   causl(e,e') causl(e,e') 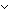 e = e' e = e' 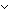 causl(e',e)) causl(e',e))
Def == & ( e:E. e:E.  (first(e)) (first(e))   ( ( e':E. loc(e') = loc(e) e':E. loc(e') = loc(e)  Id Id    causl(e',e))) causl(e',e)))
Def == & ( e:E. e:E.
Def == & (  (first(e)) (first(e))
Def == & ( 
Def == & (loc(pred(e)) = loc(e)  Id & causl(pred(e),e) Id & causl(pred(e),e)
Def == & (& ( e':E. e':E.
Def == & (& (loc(e') = loc(e)  Id Id    (causl(pred(e),e') & causl(e',e)))) (causl(pred(e),e') & causl(e',e))))
Def == & ( e:E. e:E.
Def == & (  (first(e)) (first(e))   ( ( x:Id. when(x,e) = after(x,pred(e)) x:Id. when(x,e) = after(x,pred(e))  T(loc(e),x))) T(loc(e),x)))
Def == & (Trans e,e':E. causl(e,e'))
Def == & SWellFounded(causl(e,e'))
Def == & ( e:E. e:E.
Def == & ( isrcv(kind(e)) isrcv(kind(e))
Def == & ( 
Def == & ((sends(lnk(kind(e)),sender(e)))[(index(e))]
Def == & (=
Def == & (msg(lnk(kind(e));tag(kind(e));val(e))
Def == & ( Msg(M)) Msg(M))
Def == & ( e:E. e:E.  isrcv(kind(e)) isrcv(kind(e))   causl(sender(e),e)) causl(sender(e),e))
Def == & ( e,e':E. e,e':E.
Def == & (causl(e,e')
Def == & ( 
Def == & (  (first(e')) & causl(e,pred(e')) (first(e')) & causl(e,pred(e')) 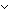 e = pred(e') e = pred(e')
Def == & (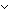  isrcv(kind(e')) & causl(e,sender(e')) isrcv(kind(e')) & causl(e,sender(e')) 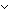 e = sender(e')) e = sender(e'))
Def == & ( e:E. e:E.  isrcv(kind(e)) isrcv(kind(e))   loc(e) = destination(lnk(kind(e)))) loc(e) = destination(lnk(kind(e))))
Def == & ( e:E, l:IdLnk. e:E, l:IdLnk.
Def == & ( loc(e) = source(l) loc(e) = source(l)   sends(l,e) = nil sends(l,e) = nil  Msg_sub(l; M) List) Msg_sub(l; M) List)
Def == & ( e,e':E. e,e':E.
Def == & ( isrcv(kind(e)) isrcv(kind(e))
Def == & ( 
Def == & ( isrcv(kind(e')) isrcv(kind(e'))
Def == & ( 
Def == & (lnk(kind(e)) = lnk(kind(e'))
Def == & ( 
Def == & ((causl(e,e')
Def == & (( 
Def == & ((causl(sender(e),sender(e'))
Def == & ((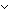 sender(e) = sender(e') sender(e) = sender(e')  E & index(e)<index(e'))) E & index(e)<index(e')))
Def == & ( e:E, l:IdLnk, n: e:E, l:IdLnk, n: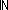 ||sends(l,e)||. ||sends(l,e)||.
Def == & (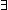 e':E. e':E.
Def == & ( isrcv(kind(e')) & lnk(kind(e')) = l & sender(e') = e & index(e') = n) isrcv(kind(e')) & lnk(kind(e')) = l & sender(e') = e & index(e') = n) |
| | | Thm*  E:Type{i}, T,V:(Id E:Type{i}, T,V:(Id  Id Id  Type{i}), M:(IdLnk Type{i}), M:(IdLnk  Id Id  Type{i}), loc:(E Type{i}), loc:(E  Id), Id),
Thm*  kind:(E kind:(E  Knd), val:(e:E Knd), val:(e:E  eventtype(kind;loc;V;M;e)), eventtype(kind;loc;V;M;e)),
Thm*  when,after:(x:Id when,after:(x:Id  e:E e:E  T(loc(e),x)), T(loc(e),x)),
Thm*  sends:(l:IdLnk sends:(l:IdLnk  E E  (Msg_sub(l; M) List)), (Msg_sub(l; M) List)),
Thm*  sender:({e:E| isrcv(kind(e)) } sender:({e:E| isrcv(kind(e)) }  E), E),
Thm*  index:(e:{e:E| isrcv(kind(e)) } index:(e:{e:E| isrcv(kind(e)) }  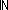 ||sends(lnk(kind(e)),sender(e))||), ||sends(lnk(kind(e)),sender(e))||),
Thm*  first:(E first:(E  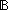 ), pred:({e':E| ), pred:({e':E|  first(e') } first(e') }  E), causl:(E E), causl:(E  E E  Prop{i}). Prop{i}).
Thm* ESAxioms{i:l}
Thm* ESAxioms(E;
Thm* ESAxioms(T;
Thm* ESAxioms(M;
Thm* ESAxioms(loc;
Thm* ESAxioms(kind;
Thm* ESAxioms(val;
Thm* ESAxioms(when;
Thm* ESAxioms(after;
Thm* ESAxioms(sends;
Thm* ESAxioms(sender;
Thm* ESAxioms(index;
Thm* ESAxioms(first;
Thm* ESAxioms(pred;
Thm* ESAxioms(causl)
Thm*  Prop{i'} Prop{i'} |
|
| Knd | Def Knd == (IdLnk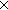 Id)+Id Id)+Id |
| | | Thm* Knd  Type Type |
|
| Msg_sub | Def Msg_sub(l; M) == {m:Msg(M)| haslink(l; m) } |
| | | Thm*  M:(IdLnk M:(IdLnk  Id Id  Type), l:IdLnk. Msg_sub(l; M) Type), l:IdLnk. Msg_sub(l; M)  Type Type |
|
| IdLnk | Def IdLnk == Id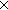 Id Id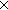 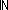 |
| | | Thm* IdLnk  Type Type |
|
| Id | Def Id == Atom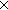 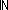 |
| | | Thm* Id  Type Type |
|
| assert | Def  b == if b b == if b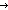 True else False fi True else False fi |
| | | Thm*  b: b: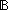 . b . b  Prop Prop |
|
| eventtype | Def eventtype(k;loc;V;M;e) == kindcase(k(e);a.V(loc(e),a);l,t.M(l,t)) |
| | | Thm*  E:Type, V:(Id E:Type, V:(Id  Id Id  Type), M:(IdLnk Type), M:(IdLnk  Id Id  Type), loc:(E Type), loc:(E  Id), k:(E Id), k:(E  Knd), Knd),
Thm*  e:E. eventtype(k;loc;V;M;e) e:E. eventtype(k;loc;V;M;e)  Type Type |
|
| iff | Def P   Q == (P Q == (P   Q) & (P Q) & (P   Q) Q) |
| | | Thm*  A,B:Prop. (A A,B:Prop. (A   B) B)  Prop Prop |
|
| int_seg | Def {i..j } == {k: } == {k: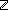 | i | i 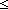 k < j } k < j } |
| | | Thm*  m,n: m,n: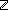 . {m..n . {m..n } }  Type Type |
|
| isrcv | Def isrcv(k) == isl(k) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)  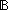 |
|
| length | Def ||as|| == Case of as; nil 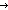 0 ; a.as' 0 ; a.as' 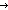 ||as'||+1 (recursive) ||as'||+1 (recursive) |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||  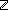 |
| | | Thm* ||nil||  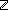 |
|
| lnk | Def lnk(k) == 1of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   lnk(k) lnk(k)  IdLnk IdLnk |
|
| strongwellfounded | Def SWellFounded(R(x;y)) == 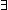 f:(T f:(T  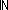 ). ).  x,y:T. R(x;y) x,y:T. R(x;y)   f(x)<f(y) f(x)<f(y) |
| | | Thm*  T:Type, R:(T T:Type, R:(T  T T  Type). SWellFounded(R(x,y)) Type). SWellFounded(R(x,y))  Prop Prop |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |
|
| tagof | Def tag(k) == 2of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   tag(k) tag(k)  Id Id |
|
| trans | Def Trans x,y:T. E(x;y) ==  a,b,c:T. E(a;b) a,b,c:T. E(a;b)   E(b;c) E(b;c)   E(a;c) E(a;c) |
| | | Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (Trans x,y:T. E(x,y)) Prop). (Trans x,y:T. E(x,y))  Prop Prop |