| | Some definitions of interest. |
|
| event_system | Def ES
Def == E:Type
Def ==  EqDecider(E) EqDecider(E) (T:Id (T:Id  Id Id  Type Type
Def ==  EqDecider(E) EqDecider(E) ( ( V:Id V:Id  Id Id  Type Type
Def ==  EqDecider(E) EqDecider(E) ( ( M:IdLnk M:IdLnk  Id Id  Type Type
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top (loc:E (loc:E  Id Id
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( kind:E kind:E  Knd Knd
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( val:(e:E val:(e:E  eventtype(kind;loc;V;M;e)) eventtype(kind;loc;V;M;e))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( when:(x:Id when:(x:Id  e:E e:E  T(loc(e),x)) T(loc(e),x))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( after:(x:Id after:(x:Id  e:E e:E  T(loc(e),x)) T(loc(e),x))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( sends:(l:IdLnk sends:(l:IdLnk  E E  (Msg_sub(l; M) List)) (Msg_sub(l; M) List))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( sender:{e:E| sender:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }  E E
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( index:(e:{e:E| index:(e:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }   ||sends ||sends
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( index:(e:{e:E| index:(e:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }   ||(lnk(kind(e)) ||(lnk(kind(e))
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( index:(e:{e:E| index:(e:{e:E|  isrcv(kind(e)) } isrcv(kind(e)) }   ||,sender(e))||) ||,sender(e))||)
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( first:E first:E  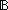
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( pred:{e':E| pred:{e':E|   (first(e')) } (first(e')) }  E E
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( causl:E causl:E  E E  Prop Prop
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms{i:l} ESAxioms{i:l}
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(E; ESAxioms(E;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(T; ESAxioms(T;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(M; ESAxioms(M;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(loc; ESAxioms(loc;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(kind; ESAxioms(kind;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(val; ESAxioms(val;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(when; ESAxioms(when;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(after; ESAxioms(after;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(sends; ESAxioms(sends;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(sender; ESAxioms(sender;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(index; ESAxioms(index;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(first; ESAxioms(first;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(pred; ESAxioms(pred;
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( ESAxioms(causl) ESAxioms(causl)
Def ==  EqDecider(E) EqDecider(E) ( ( Top Top ( ( Top)) Top)) |
| | | Thm* ES  Type{i'} Type{i'} |
|
| Knd | Def Knd == (IdLnk Id)+Id Id)+Id |
| | | Thm* Knd  Type Type |
|
| IdLnk | Def IdLnk == Id Id Id  |
| | | Thm* IdLnk  Type Type |
|
| Id | Def Id == Atom  |
| | | Thm* Id  Type Type |
|
| assert | Def  b == if b b == if b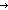 True else False fi True else False fi |
| | | Thm*  b: b: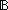 . b . b  Prop Prop |
|
| es-E | Def E == 1of(es) |
|
| es-kind | Def kind(e) == 1of(2of(2of(2of(2of(2of(2of(2of(es))))))))(e) |
|
| es-loc | Def loc(e) == 1of(2of(2of(2of(2of(2of(2of(es)))))))(e) |
|
| es-sender | Def sender(e)
Def == 1of(2of(2of(2of(2of(2of(2of(2of(2of(2of(2of(2of(2of(es)))))))))))))(e) |
|
| isrcv | Def isrcv(k) == isl(k) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)  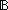 |
|
| lnk | Def lnk(k) == 1of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   lnk(k) lnk(k)  IdLnk IdLnk |
|
| lsrc | Def source(l) == 1of(l) |
| | | Thm*  l:IdLnk. source(l) l:IdLnk. source(l)  Id Id |
|
| tagof | Def tag(k) == 2of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   tag(k) tag(k)  Id Id |
|
| outl | Def outl(x) == InjCase(x; y. y; z. "???") |
| | | Thm*  A,B:Type, x:A+B. isl(x) A,B:Type, x:A+B. isl(x)   outl(x) outl(x)  A A |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |
|
| rcv | Def rcv(l; tg) == inl(<l,tg>) |
| | | Thm*  l:IdLnk, tg:Id. rcv(l; tg) l:IdLnk, tg:Id. rcv(l; tg)  Knd Knd |