Selected Objects
| def | es-ble |
es-ble{i:l}(es;e;e')
== InjCase(decidable__es_DASH_le{1:l, i:l}(es,e',e); x. true , false , false ) ) |
| THM | assert-es-ble |
 es:ES, e,e':E. es-ble{i:l}(es;e;e') es:ES, e,e':E. es-ble{i:l}(es;e;e') 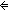  e e  e' e' |
| def | es-mtag |
mtag(m) == mtag(m) |
| def | es-before |
before(e) == if first(e)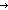 nil else before(pred(e)) @ [pred(e)] fi (recursive) nil else before(pred(e)) @ [pred(e)] fi (recursive) |
| THM | member-es-before |
 the_es:ES, e',e:E. (e the_es:ES, e',e:E. (e  before(e')) before(e')) 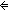  (e <loc e') (e <loc e') |
| def | es-interval |
[e, e'] == filter( ev.es-ble{i:l}(es;e;ev);before(e') @ [e']) ev.es-ble{i:l}(es;e;ev);before(e') @ [e']) |
| THM | member-es-interval |
 es:ES, e,e',ev:E. (ev es:ES, e,e',ev:E. (ev  [e, e']) [e, e']) 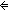  e e  ev & ev ev & ev  e' e' |
| def | es-tg-sends |
sends(l,tg,e) == filter( m.mtag(m) = tg;sends(l;e)) m.mtag(m) = tg;sends(l;e)) |
| THM | es-after-pred |
 es:ES, x:Id, e:E. es:ES, x:Id, e:E.
 first(e) first(e)   (x after pred(e)) = (x when e) (x after pred(e)) = (x when e)  vartype(loc(e);x) vartype(loc(e);x) |
| def | alle-at |
 e@i.P(e) == e@i.P(e) ==  e:E. loc(e) = i e:E. loc(e) = i  Id Id   P(e) P(e) |
| def | alle-at1 |
@i always.P(v) ==  e@i.P((x when e)) e@i.P((x when e)) |
| THM | alle-at-iff |
 es:ES, i:Id, P:({e:E| loc(e) = i es:ES, i:Id, P:({e:E| loc(e) = i  Id } Id }  Prop). Prop).
 e@i.P(e) e@i.P(e) 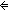   e@i.first(e) e@i.first(e)   P(e) & P(e) &  e@i. e@i. first(e) first(e)   P(pred(e)) P(pred(e))   P(e) P(e) |
| THM | es-invariant1 |
 es:ES, i,x:Id, T:Type, I:(T es:ES, i,x:Id, T:Type, I:(T  Prop). Prop).
(vartype(i;x) 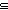 r T) & r T) &  e@i.first(e) e@i.first(e)   I((x when e)) I((x when e))
 
 e@i.I((x when e)) e@i.I((x when e))   I((x after e)) I((x after e))   @i always.I(x) @i always.I(x) |
| def | existse-at |
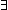 e@i.P(e) == e@i.P(e) == 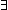 e:E. loc(e) = i e:E. loc(e) = i  Id & P(e) Id & P(e) |
| THM | change-lemma |
 es:ES, x,i:Id, T:Type. es:ES, x,i:Id, T:Type.
( x,y:T. Dec(x = y x,y:T. Dec(x = y  T)) T))
 
(vartype(i;x) 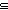 r T) r T)
 
( e',e:E. e',e:E.
(e  e' e'
( 
(loc(e') = i  Id Id
( 
( (x after e') = (x when e) (x after e') = (x when e)  T T
( 
((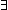 ev:E. e ev:E. e  ev & ev ev & ev  e' & e' &  (x after ev) = (x when ev) (x after ev) = (x when ev)  T)) T)) |
| THM | es-first-exists |
 es:ES, e':E. es:ES, e':E. 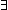 e:E. first(e) & e e:E. first(e) & e  e' e' |
| THM | change-since-init |
 es:ES, x,i:Id, T:Type, c:T. es:ES, x,i:Id, T:Type, c:T.
( x,y:T. Dec(x = y x,y:T. Dec(x = y  T)) T))
 
(vartype(i;x) 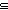 r T) r T)
 
( e:E. loc(e) = i e:E. loc(e) = i  Id Id   first(e) first(e)   (x when e) = c (x when e) = c  T) T)
 
( e':E. e':E.
(loc(e') = i  Id Id
( 
( (x after e') = c (x after e') = c  T T   ( (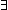 ev:E. ev ev:E. ev  e' & e' &  (x after ev) = (x when ev) (x after ev) = (x when ev)  T)) T)) |
| THM | es-rcv-kind |
 es:ES, l:IdLnk, tg:Id, e:E. es:ES, l:IdLnk, tg:Id, e:E.
isrcv(e)   lnk(e) = l lnk(e) = l   tag(e) = tg tag(e) = tg   kind(e) = rcv(l; tg) kind(e) = rcv(l; tg) |
| THM | es-kind-rcv |
 es:ES, l:IdLnk, tg:Id, e:E. es:ES, l:IdLnk, tg:Id, e:E.
kind(e) = rcv(l; tg)
 
isrcv(e) & lnk(e) = l & tag(e) = tg & loc(sender(e)) = source(l) |
| def | action |
action(dec) == Unit+(k:Knd dec(k)) dec(k)) |
| def | w-action-dec |
w-action-dec(TA;M;i)(k)
== kindcase(k;a.TA(i,a);l,tg.if destination(l) = i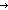 M(l,tg) else Void fi) M(l,tg) else Void fi) |
| def | world |
World
== T:Id  Id Id  Type Type
==  TA:Id TA:Id  Id Id  Type Type
==  M:IdLnk M:IdLnk  Id Id  Type Type
==  (i:Id (i:Id     (x:Id (x:Id  T(i,x))) T(i,x))) (i:Id (i:Id     action(w-action-dec(TA;M;i))) action(w-action-dec(TA;M;i)))
== (i:Id     ({m:Msg(M)| source(mlnk(m)) = i } List)) ({m:Msg(M)| source(mlnk(m)) = i } List)) Top Top |
| def | w-T |
w.T == 1of(w) |
| def | w-TA |
w.TA == 1of(2of(w)) |
| def | w-M |
w.M == 1of(2of(2of(w))) |
| def | w-vartype |
vartype(i;x) == w.T(i,x) |
| def | w-action |
Action(i) == action(w-action-dec(w.TA;w.M;i)) |
| def | w-isnull |
isnull(a) == isl(a) |
| def | w-kind |
kind(a) == 1of(outr(a)) |
| def | w-valtype |
valtype(i;a) == kindcase(kind(a);a.w.TA(i,a);l,tg.w.M(l,tg)) |
| def | w-val |
val(a) == 2of(outr(a)) |
| def | w-isrcvl |
isrcv(l;a) ==   isnull(a) isnull(a)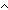  isrcv(kind(a)) isrcv(kind(a))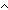  lnk(kind(a)) = l lnk(kind(a)) = l |
| THM | assert-w-isrcvl |
 the_w:World, l:IdLnk, i:Id, a:Action(i). the_w:World, l:IdLnk, i:Id, a:Action(i).
isrcv(l;a)    isnull(a) & isrcv(kind(a)) & lnk(kind(a)) = l isnull(a) & isrcv(kind(a)) & lnk(kind(a)) = l |
| def | w-Msg |
Msg == Msg(w.M) |
| def | w-s |
s(i;t).x == 1of(2of(2of(2of(w))))(i,t,x) |
| def | w-a |
a(i;t) == 1of(2of(2of(2of(2of(w)))))(i,t) |
| def | w-m |
m(i;t) == 1of(2of(2of(2of(2of(2of(w))))))(i,t) |
| def | w-onlnk |
onlnk(l;mss) == filter( ms.mlnk(ms) = l;mss) ms.mlnk(ms) = l;mss) |
| THM | w-onlnk-m |
 w:World, t: w:World, t: , l:IdLnk, i:Id. ||onlnk(l;m(i;t))|| , l:IdLnk, i:Id. ||onlnk(l;m(i;t))||  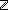 |
| def | w-withlnk |
withlnk(l;mss) == mapfilter( ms.2of(ms); ms.2of(ms); ms.mlnk(ms) = l;mss) ms.mlnk(ms) = l;mss) |
| def | w-tagged |
w-tagged(tg; mss) == filter( ms.mtag(ms) = tg;mss) ms.mtag(ms) = tg;mss) |
| def | w-ml |
m(l;t) == onlnk(l;m(source(l);t)) |
| def | w-snds |
snds(l;t) == concat(map( t1.m(l;t1);upto(t))) t1.m(l;t1);upto(t))) |
| def | w-rcvs |
rcvs(l;t) == filter( a.isrcv(l;a);map( a.isrcv(l;a);map( t1.a(destination(l);t1);upto(t))) t1.a(destination(l);t1);upto(t))) |
| def | w-queue |
queue(l;t) == nth_tl(||rcvs(l;t)||;snds(l;t)) |
| def | w-msg |
msg(a) == msg(lnk(kind(a));tag(kind(a));val(a)) |
| def | fair-fifo |
FairFifo
== ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.  source(l) = i source(l) = i   onlnk(l;m(i;t)) = nil onlnk(l;m(i;t)) = nil  Msg List) Msg List)
== & ( i:Id, t: i:Id, t: . .
== & ( isnull(a(i;t)) isnull(a(i;t))
== & ( 
== & (( x:Id. s(i;t+1).x = s(i;t).x x:Id. s(i;t+1).x = s(i;t).x  vartype(i;x)) & m(i;t) = nil vartype(i;x)) & m(i;t) = nil  Msg List) Msg List)
== & ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.
== & ( isrcv(l;a(i;t)) isrcv(l;a(i;t))
== & ( 
== & (destination(l) = i
== & (& ||queue(l;t)||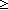 1 & hd(queue(l;t)) = msg(a(i;t)) 1 & hd(queue(l;t)) = msg(a(i;t))  Msg) Msg)
== & ( l:IdLnk, t: l:IdLnk, t: . .
== & (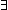 t': t': . .
== & (t t' & t' &  isrcv(l;a(destination(l);t')) isrcv(l;a(destination(l);t')) 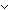 queue(l;t') = nil queue(l;t') = nil  Msg List) Msg List) |
| def | w-E |
E == {p:(Id  )| )|   isnull(a(1of(p);2of(p))) } isnull(a(1of(p);2of(p))) } |
| def | w-eq-E |
p = q == 1of(p) = 1of(q)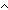  (2of(p)= (2of(p)= 2of(q)) 2of(q)) |
| THM | assert-w-eq-E |
 the_w:World, e,e':E. e = e' the_w:World, e,e':E. e = e'   e = e' e = e' |
| THM | assert-w-eq-E-iff |
 the_w:World, e,e':E. e = e' the_w:World, e,e':E. e = e' 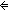  e = e' e = e' |
| def | w-loc |
loc(e) == 1of(e) |
| def | w-act |
act(e) == a(1of(e);2of(e)) |
| THM | w-act-not-null |
 the_w:World, e:E. the_w:World, e:E.  isnull(act(e)) isnull(act(e)) |
| def | w-ekind |
kind(e) == kind(act(e)) |
| def | w-V |
V(i;k) == kindcase(k;a.1of(2of(w))(i,a);l,tg.1of(2of(2of(w)))(l,tg)) |
| def | w-eval |
val(e) == val(act(e)) |
| def | w-time |
time(e) == 2of(e) |
| def | w-when |
(x when e) == s(1of(e);2of(e)).x |
| def | w-after |
(x after e) == s(1of(e);2of(e)+1).x |
| def | w-initially |
(x initially i) == s(i;0).x |
| def | w-first |
first(e)
== if time(e)= 0 0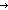 true true
== i; isnull(a(loc(e);time(e)-1))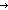 first(<loc(e),time(e)-1>) first(<loc(e),time(e)-1>)
== else false fi fi
(recursive) |
| THM | w-first-aux |
 the_w:World, i:Id, t: the_w:World, i:Id, t: . first(<i,t>) . first(<i,t>)  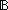 |
| THM | assert-w-first |
 the_w:World, e:E. first(e) the_w:World, e:E. first(e) 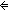  ( ( t': t': . t'<time(e) . t'<time(e)   isnull(a(loc(e);t'))) isnull(a(loc(e);t'))) |
| THM | w-loc-time |
 the_w:World, e:E. <loc(e),time(e)> ~ e the_w:World, e:E. <loc(e),time(e)> ~ e |
| def | w-pred |
pred(e)
== if isnull(a(loc(e);time(e)-1))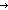 pred(<loc(e),time(e)-1>) pred(<loc(e),time(e)-1>)
== else <loc(e),time(e)-1> fi
(recursive) |
| THM | w-pred-aux |
 the_w:World, t: the_w:World, t: , i:Id. , i:Id.  first(<i,t>) first(<i,t>)   pred(<i,t>) pred(<i,t>)  E E |
| def | w-locl |
e <loc e' == loc(e) = loc(e')  Id & time(e)<time(e') Id & time(e)<time(e') |
| def | w-sends |
sends(l;e) == onlnk(l;m(loc(e);time(e))) |
| def | w-match |
match(l;t;t')
== (||snds(l;t)||  ||rcvs(l;t')||) ||rcvs(l;t')||)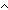 
== (||rcvs(l;t')||< ||snds(l;t)||+||onlnk(l;m(source(l);t))||) ||snds(l;t)||+||onlnk(l;m(source(l);t))||) |
| THM | assert-w-match |
 the_w:World, l:IdLnk, t,t': the_w:World, l:IdLnk, t,t': . .
match(l;t;t')
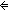 
||snds(l;t)|| ||rcvs(l;t')|| ||rcvs(l;t')||
& ||rcvs(l;t')||<||snds(l;t)||+||onlnk(l;m(source(l);t))|| |
| THM | w-match-exists |
 the_w:World, e:E. the_w:World, e:E.
FairFifo   isrcv(kind(e)) isrcv(kind(e))   ( (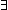 t: t: time(e). match(lnk(kind(e));t;time(e))) time(e). match(lnk(kind(e));t;time(e))) |
| THM | better-w-match-exists |
 the_w:World, e:E. the_w:World, e:E.
FairFifo
 
isrcv(kind(e))
 
(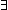 t: t: time(e). time(e).
(match(lnk(kind(e));t;time(e))
(& onlnk(lnk(kind(e));m(source(lnk(kind(e)));t))[(||rcvs(lnk(kind(e));time(e))||
(& -||snds(lnk(kind(e));t)||)]
(& =
(& msg(a(loc(e);time(e)))
(&  Msg) Msg) |
| THM | w-match-unique |
 the_w:World, e:E, t,t': the_w:World, e:E, t,t': . .
FairFifo
 
isrcv(kind(e))
 
match(lnk(kind(e));t;time(e))   match(lnk(kind(e));t';time(e)) match(lnk(kind(e));t';time(e))   t = t' t = t' |
| THM | w-match-property |
 the_w:World, e:E, t: the_w:World, e:E, t: . .
FairFifo
 
isrcv(kind(e))
 
match(lnk(kind(e));t;time(e))
 
onlnk(lnk(kind(e));m(source(lnk(kind(e)));t))[(||rcvs(lnk(kind(e));time(e))||
-||snds(lnk(kind(e));t)||)]
=
msg(a(loc(e);time(e)))
 Msg Msg |
| def | w-sender |
sender(e) == <source(lnk(kind(e))),mu( t.match(lnk(kind(e));t;time(e)))> t.match(lnk(kind(e));t;time(e)))> |
| def | w-index |
index(e)
== ||rcvs(lnk(kind(e));time(e))||-||snds(lnk(kind(e));time(sender(e)))|| |
| def | w-causl |
e <c e' == e  e,e'. e <loc e' e,e'. e <loc e' 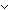  isrcv(kind(e')) & e = sender(e') isrcv(kind(e')) & e = sender(e')  E^+ e' E^+ e' |
| THM | w-causl-time |
 the_w:World, e,e':E. FairFifo the_w:World, e,e':E. FairFifo   e <c e' e <c e'   time(e)<time(e') time(e)<time(e') |
| THM | w-locl-iff |
 the_w:World, e,e':E. FairFifo the_w:World, e,e':E. FairFifo   (e <loc e' (e <loc e' 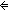  loc(e) = loc(e') loc(e) = loc(e')  Id & e <c e') Id & e <c e') |
| THM | world-event-system |
 the_w:World. the_w:World.
FairFifo
 
ESAxioms{i:l}
ESAxioms(E;
ESAxioms(( i,x. vartype(i;x)); i,x. vartype(i;x));
ESAxioms(the_w.M;
ESAxioms(( e.loc(e)); e.loc(e));
ESAxioms(( e.kind(e)); e.kind(e));
ESAxioms(( e.val(e)); e.val(e));
ESAxioms(( x,e. (x when e)); x,e. (x when e));
ESAxioms(( x,e. (x after e)); x,e. (x after e));
ESAxioms(( l,e. sends(l;e)); l,e. sends(l;e));
ESAxioms(( e.sender(e)); e.sender(e));
ESAxioms(( e.index(e)); e.index(e));
ESAxioms(( e.first(e)); e.first(e));
ESAxioms(( e.pred(e)); e.pred(e));
ESAxioms(( e,e'. e <c e')) e,e'. e <c e')) |
| def | w-es |
ES(the_w;p)
== <E
== ,product-deq(Id; ;IdDeq;NatDeq) ;IdDeq;NatDeq)
== ,( i,x. vartype(i;x)) i,x. vartype(i;x))
== ,( i,a. V(i;locl(a))) i,a. V(i;locl(a)))
== ,the_w.M
== ,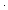
== ,( e.loc(e)) e.loc(e))
== ,( e.kind(e)) e.kind(e))
== ,( e.val(e)) e.val(e))
== ,( x,e. (x when e)) x,e. (x when e))
== ,( x,e. (x after e)) x,e. (x after e))
== ,( l,e. sends(l;e)) l,e. sends(l;e))
== ,( e.sender(e)) e.sender(e))
== ,( e.index(e)) e.index(e))
== ,( e.first(e)) e.first(e))
== ,( e.pred(e)) e.pred(e))
== ,( e,e'. e <c e') e,e'. e <c e')
== ,world_DASH_event_DASH_system{1:l, i:l}(the_w,p)
== ,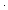 > > |
| THM | es-valtype-w-valtype |
 i:Id, w:World, p:FairFifo, t: i:Id, w:World, p:FairFifo, t: . .
 isnull(a(i;t)) isnull(a(i;t))   (valtype(<i,t>) ~ valtype(i;a(i;t))) (valtype(<i,t>) ~ valtype(i;a(i;t))) |
| def | fpf |
a:A fp-> B(a) == d:A List a:{a:A| (a a:{a:A| (a  d) } d) }  B(a) B(a) |
| THM | subtype-fpf2 |
 B1,B2:(A B1,B2:(A  Type). ( Type). ( a:A. B1(a) a:A. B1(a) 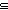 r B2(a)) r B2(a))   (a:A fp-> B1(a) (a:A fp-> B1(a) 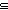 r a:A fp-> B2(a)) r a:A fp-> B2(a)) |
| THM | subtype-fpf3 |
 B1:(A1 B1:(A1  Type), B2:(A2 Type), B2:(A2  Type). Type).
strong-subtype(A1;A2)
 
( a:A1. B1(a) a:A1. B1(a) 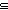 r B2(a)) r B2(a))   (a:A1 fp-> B1(a) (a:A1 fp-> B1(a) 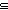 r a:A2 fp-> B2(a)) r a:A2 fp-> B2(a)) |
| def | fpf-dom |
x  dom(f) == deq-member(eq;x;1of(f)) dom(f) == deq-member(eq;x;1of(f)) |
| THM | fpf-dom_functionality |
 B:(A B:(A  Type), eq1,eq2:EqDecider(A), f:a:A fp-> B(a), x:A. Type), eq1,eq2:EqDecider(A), f:a:A fp-> B(a), x:A.
x  dom(f) = x dom(f) = x  dom(f) dom(f)  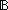 |
| THM | fpf-dom_functionality2 |
 eq1,eq2:EqDecider(A), f:a:A fp-> Top, x:A. x eq1,eq2:EqDecider(A), f:a:A fp-> Top, x:A. x  dom(f) dom(f)   x x  dom(f) dom(f) |
| THM | fpf-dom-type |
 eq:EqDecider(Y), f:x:X fp-> Top, x:Y. eq:EqDecider(Y), f:x:X fp-> Top, x:Y.
strong-subtype(X;Y)   x x  dom(f) dom(f)   x x  X X |
| THM | fpf-dom-type2 |
 eq:EqDecider(Y), f:x:X fp-> Top, x:Y. eq:EqDecider(Y), f:x:X fp-> Top, x:Y.
strong-subtype(X;Y)   x x  dom(f) dom(f)   x x  X X |
| def | fpf-empty |
== <nil, x. x. > > |
| def | fpf-is-empty |
fpf-is-empty(f) == ||1of(f)||= 0 0 |
| THM | assert-fpf-is-empty |
 B:(A B:(A  Type), f:x:A fp-> B(x). fpf-is-empty(f) Type), f:x:A fp-> B(x). fpf-is-empty(f) 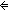  f = f =  x:A fp-> B(x) x:A fp-> B(x) |
| def | fpf-ap |
f(x) == 2of(f)(x) |
| def | fpf-cap |
f(x)?z == if x  dom(f) dom(f)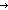 f(x) else z fi f(x) else z fi |
| def | fpf-val |
z != f(x) ==> P(a;z) ==  x x  dom(f) dom(f)   P(x;f(x)) P(x;f(x)) |
| def | fpf-sub |
f 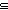 g == g ==  x:A. x:A.  x x  dom(f) dom(f)    x x  dom(g) & f(x) = g(x) dom(g) & f(x) = g(x)  B(x) B(x) |
| THM | fpf-empty-sub |
 B,eq,g:Top. B,eq,g:Top. 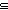 g g |