| | Some definitions of interest. |
|
| w-action | Def Action(i) == action(w-action-dec(w.TA;w.M;i)) |
|
| world | Def World
Def == T:Id  Id Id  Type Type
Def ==  TA:Id TA:Id  Id Id  Type Type
Def ==  M:IdLnk M:IdLnk  Id Id  Type Type
Def ==  (i:Id (i:Id     (x:Id (x:Id  T(i,x))) T(i,x))) (i:Id (i:Id     action(w-action-dec(TA;M;i))) action(w-action-dec(TA;M;i)))
Def == (i:Id     ({m:Msg(M)| source(mlnk(m)) = i } List)) ({m:Msg(M)| source(mlnk(m)) = i } List)) Top Top |
| | | Thm* World  Type{i'} Type{i'} |
|
| Id | Def Id == Atom  |
| | | Thm* Id  Type Type |
|
| assert | Def  b == if b b == if b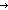 True else False fi True else False fi |
| | | Thm*  b: b: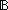 . b . b  Prop Prop |
|
| not | Def  A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. ( A) A)  Prop Prop |
|
| w-isnull | Def isnull(a) == isl(a) |
|
| w-val | Def val(a) == 2of(outr(a)) |
|
| w-valtype | Def valtype(i;a) == kindcase(kind(a);a.w.TA(i,a);l,tg.w.M(l,tg)) |