| | Some definitions of interest. |
|
| fair-fifo | Def FairFifo
Def == ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.  source(l) = i source(l) = i   onlnk(l;m(i;t)) = nil onlnk(l;m(i;t)) = nil  Msg List) Msg List)
Def == & ( i:Id, t: i:Id, t: . .
Def == & ( isnull(a(i;t)) isnull(a(i;t))
Def == & ( 
Def == & (( x:Id. s(i;t+1).x = s(i;t).x x:Id. s(i;t+1).x = s(i;t).x  vartype(i;x)) vartype(i;x))
Def == & (& m(i;t) = nil  Msg List) Msg List)
Def == & ( i:Id, t: i:Id, t: , l:IdLnk. , l:IdLnk.
Def == & ( isrcv(l;a(i;t)) isrcv(l;a(i;t))
Def == & ( 
Def == & (destination(l) = i
Def == & (& ||queue(l;t)||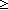 1 & hd(queue(l;t)) = msg(a(i;t)) 1 & hd(queue(l;t)) = msg(a(i;t))  Msg) Msg)
Def == & ( l:IdLnk, t: l:IdLnk, t: . .
Def == & (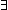 t': t': . .
Def == & (t t' & t' &  isrcv(l;a(destination(l);t')) isrcv(l;a(destination(l);t')) 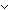 queue(l;t') = nil queue(l;t') = nil  Msg List) Msg List) |
|
| w-E | Def E == {p:(Id  )| )|   isnull(a(1of(p);2of(p))) } isnull(a(1of(p);2of(p))) } |
|
| w-sender | Def sender(e) == <source(lnk(kind(e))),mu( t.match(lnk(kind(e));t;time(e)))> t.match(lnk(kind(e));t;time(e)))> |
|
| w-match | Def match(l;t;t')
Def == (||snds(l;t)||  ||rcvs(l;t')||) ||rcvs(l;t')||)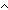 
Def == (||rcvs(l;t')||< ||snds(l;t)||+||onlnk(l;m(source(l);t))||) ||snds(l;t)||+||onlnk(l;m(source(l);t))||) |
|
| world | Def World
Def == T:Id  Id Id  Type Type
Def ==  TA:Id TA:Id  Id Id  Type Type
Def ==  M:IdLnk M:IdLnk  Id Id  Type Type
Def ==  (i:Id (i:Id     (x:Id (x:Id  T(i,x))) T(i,x))) (i:Id (i:Id     action(w-action-dec(TA;M;i))) action(w-action-dec(TA;M;i)))
Def == (i:Id     ({m:Msg(M)| source(mlnk(m)) = i } List)) ({m:Msg(M)| source(mlnk(m)) = i } List)) Top Top |
| | | Thm* World  Type{i'} Type{i'} |
|
| assert | Def  b == if b b == if b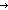 True else False fi True else False fi |
| | | Thm*  b: b: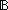 . b . b  Prop Prop |
|
| isrcv | Def isrcv(k) == isl(k) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)  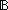 |
|
| lnk | Def lnk(k) == 1of(outl(k)) |
| | | Thm*  k:Knd. isrcv(k) k:Knd. isrcv(k)   lnk(k) lnk(k)  IdLnk IdLnk |
|
| nat | Def  == {i: == {i: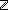 | 0 | 0 i } i } |
| | | Thm*   Type Type |
|
| w-ekind | Def kind(e) == kind(act(e)) |
|
| w-time | Def time(e) == 2of(e) |