| Rank | Theorem | Name |
| 6 | Thm*  the_w:World. the_w:World.
Thm* FairFifo
Thm*  
Thm* ESAxioms{i:l}
Thm* ESAxioms(E;
Thm* ESAxioms(( i,x. vartype(i;x)); i,x. vartype(i;x));
Thm* ESAxioms(the_w.M;
Thm* ESAxioms(( e.loc(e)); e.loc(e));
Thm* ESAxioms(( e.kind(e)); e.kind(e));
Thm* ESAxioms(( e.val(e)); e.val(e));
Thm* ESAxioms(( x,e. (x when e)); x,e. (x when e));
Thm* ESAxioms(( x,e. (x after e)); x,e. (x after e));
Thm* ESAxioms(( l,e. sends(l;e)); l,e. sends(l;e));
Thm* ESAxioms(( e.sender(e)); e.sender(e));
Thm* ESAxioms(( e.index(e)); e.index(e));
Thm* ESAxioms(( e.first(e)); e.first(e));
Thm* ESAxioms(( e.pred(e)); e.pred(e));
Thm* ESAxioms(( e,e'. e <c e')) e,e'. e <c e')) | [world-event-system] |
| cites the following: |
| 0 | Thm*  the_w:World, e:E. the_w:World, e:E.  isnull(act(e)) isnull(act(e)) | [w-act-not-null] |
| 1 | Thm*  the_w:World, e:E. first(e) the_w:World, e:E. first(e) 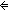  ( ( t': t': . t'<time(e) . t'<time(e)   isnull(a(loc(e);t'))) isnull(a(loc(e);t'))) | [assert-w-first] |
| 0 | Thm*  the_w:World, t: the_w:World, t: , i:Id. , i:Id.  first(<i,t>) first(<i,t>)   pred(<i,t>) pred(<i,t>)  E E | [w-pred-aux] |
| 0 | Thm*  the_w:World, i:Id, t: the_w:World, i:Id, t: . first(<i,t>) . first(<i,t>)  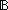 | [w-first-aux] |
| 0 | Thm*  the_w:World, e:E. <loc(e),time(e)> ~ e the_w:World, e:E. <loc(e),time(e)> ~ e | [w-loc-time] |
| 1 | Thm*  R:(T R:(T  T T  Prop). Trans x,y:T. x R^+ y Prop). Trans x,y:T. x R^+ y | [rel_plus_trans] |
| 4 | Thm*  the_w:World, e,e':E. FairFifo the_w:World, e,e':E. FairFifo   e <c e' e <c e'   time(e)<time(e') time(e)<time(e') | [w-causl-time] |
| 5 | Thm*  the_w:World, e:E, t: the_w:World, e:E, t: . .
Thm* FairFifo
Thm*  
Thm* isrcv(kind(e))
Thm*  
Thm* match(lnk(kind(e));t;time(e))
Thm*  
Thm* onlnk(lnk(kind(e));m(source(lnk(kind(e)));t))[(||rcvs(lnk(kind(e));time(e))||
Thm* -||snds(lnk(kind(e));t)||)]
Thm* =
Thm* msg(a(loc(e);time(e)))
Thm*  Msg Msg | [w-match-property] |
| 0 | Thm*  R:(T R:(T  T T  Prop), x,y:T. (x R^+ y) Prop), x,y:T. (x R^+ y)   (x R y) (x R y) 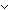 ( (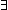 z:T. (x R^+ z) & (z R y)) z:T. (x R^+ z) & (z R y)) | [rel_plus_implies] |
| 0 | Thm*  T:Type, P:(T T:Type, P:(T  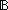 ), l:T List. filter(P;l) ), l:T List. filter(P;l)  {x:T| P(x) } List {x:T| P(x) } List | [filter_type] |
| 3 | Thm*  the_w:World, e:E. the_w:World, e:E.
Thm* FairFifo   isrcv(kind(e)) isrcv(kind(e))   ( (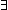 t: t: time(e). match(lnk(kind(e));t;time(e))) time(e). match(lnk(kind(e));t;time(e))) | [w-match-exists] |
| 4 | Thm*  i,j: i,j: . .
Thm* i<j
Thm*  
Thm* ( f:( f:(   T), P:(T T), P:(T  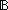 ). ).
Thm* (P(f(i))   ||filter(P;map(f;upto(i)))||<||filter(P;map(f;upto(j)))||) ||filter(P;map(f;upto(i)))||<||filter(P;map(f;upto(j)))||) | [filter_map_upto] |
| 5 | Thm*  the_w:World, e,e':E. the_w:World, e,e':E.
Thm* FairFifo   (e <loc e' (e <loc e' 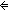  loc(e) = loc(e') loc(e) = loc(e')  Id & e <c e') Id & e <c e') | [w-locl-iff] |
| 0 | Thm*  P:(T P:(T  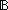 ), A:T List, B:Top. filter(P;A @ B) ~ (filter(P;A) @ filter(P;B)) ), A:T List, B:Top. filter(P;A @ B) ~ (filter(P;A) @ filter(P;B)) | [filter_append_sq] |
| 1 | Thm*  P:(T P:(T  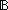 ), L2,L1:T List. L1 ), L2,L1:T List. L1  L2 L2   filter(P;L1) filter(P;L1)  filter(P;L2) filter(P;L2) | [filter_iseg] |
| 1 | Thm*  r: r: , L:Top List. ||nth_tl(r;L)|| = if r< , L:Top List. ||nth_tl(r;L)|| = if r< ||L|| ||L||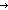 ||L||-r else 0 fi ||L||-r else 0 fi | [general_length_nth_tl] |
| 2 | Thm*  i,j: i,j: . i . i j j   upto(i) upto(i)  upto(j) upto(j) | [upto_iseg] |
| 0 | Thm*  f:(A f:(A  B), L1,L2:A List. L1 B), L1,L2:A List. L1  L2 L2   map(f;L1) map(f;L1)  map(f;L2) map(f;L2) | [iseg_map] |
| 2 | Thm*  ll1,ll2:(T List) List. ll1 ll1,ll2:(T List) List. ll1  ll2 ll2   concat(ll1) concat(ll1)  concat(ll2) concat(ll2) | [concat_iseg] |
| 1 | Thm*  l1,l2:T List. l1 l1,l2:T List. l1  l2 l2   ||l1|| ||l1|| ||l2|| ||l2|| | [iseg_length] |
| 0 | Thm*  f,as':Top, A:Type, as:A List. map(f;as @ as') ~ (map(f;as) @ map(f;as')) f,as':Top, A:Type, as:A List. map(f;as @ as') ~ (map(f;as) @ map(f;as')) | [map_append_sq] |
| 0 | Thm*  l:T List. (l @ nil) ~ l l:T List. (l @ nil) ~ l | [append_nil_sq] |
| 0 | Thm*  l:Top List, ll:(Top List) List. concat([l / ll]) ~ (l @ concat(ll)) l:Top List, ll:(Top List) List. concat([l / ll]) ~ (l @ concat(ll)) | [concat-cons] |
| 1 | Thm*  ll1,ll2:(Top List) List. concat(ll1 @ ll2) ~ (concat(ll1) @ concat(ll2)) ll1,ll2:(Top List) List. concat(ll1 @ ll2) ~ (concat(ll1) @ concat(ll2)) | [concat_append] |
| 0 | Thm*  as,bs:T List. ||as @ bs|| = ||as||+||bs|| as,bs:T List. ||as @ bs|| = ||as||+||bs||  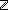 | [length_append] |
| 1 | Thm*  t',m: t',m: , T:Type, f:( , T:Type, f:(   T), P:(T T), P:(T  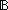 ). ).
Thm* m+1 ||filter(P;map(f;upto(t')))|| ||filter(P;map(f;upto(t')))||
Thm*  
Thm* (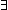 t: t: . P(f(t)) & ||filter(P;map(f;upto(t)))|| = m . P(f(t)) & ||filter(P;map(f;upto(t)))|| = m  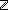 ) ) | [filter_map_upto2] |
| 0 | Thm*  the_w:World, l:IdLnk, t,t': the_w:World, l:IdLnk, t,t': . .
Thm* match(l;t;t')
Thm* 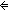 
Thm* ||snds(l;t)|| ||rcvs(l;t')|| ||rcvs(l;t')||
Thm* & ||rcvs(l;t')||<||snds(l;t)||+||onlnk(l;m(source(l);t))|| | [assert-w-match] |
| 0 | Thm*  w:World, t: w:World, t: , l:IdLnk, i:Id. ||onlnk(l;m(i;t))|| , l:IdLnk, i:Id. ||onlnk(l;m(i;t))||  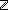 | [w-onlnk-m] |
| 0 | Thm*  f:( f:(   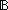 ). ( ). (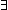 n: n: . f(n)) . f(n))   f(mu(f)) & ( f(mu(f)) & ( i: i: . i<mu(f) . i<mu(f)    f(i)) f(i)) | [mu-property] |
| 4 | Thm*  the_w:World, e:E, t,t': the_w:World, e:E, t,t': . .
Thm* FairFifo
Thm*  
Thm* isrcv(kind(e))
Thm*  
Thm* match(lnk(kind(e));t;time(e))   match(lnk(kind(e));t';time(e)) match(lnk(kind(e));t';time(e))   t = t' t = t' | [w-match-unique] |