Thm*  x:Id, L:Knd List, t:Type. t x:Id, L:Knd List, t:Type. t   Feasible(only members of L affect x :t) Feasible(only members of L affect x :t) | [ma-single-frame-feasible] |
Thm*  ltg:(IdLnk ltg:(IdLnk Id Id Type), i:Id. (ltg Type), i:Id. (ltg  da-outlinks(;i)) da-outlinks(;i))   False False | [da-outlinks-empty] |
Thm*  eq:EqDecider(A), x:A, v,P:Top. z != x : v(x) ==> P(a,z) ~ (True eq:EqDecider(A), x:A, v,P:Top. z != x : v(x) ==> P(a,z) ~ (True   P(x,v)) P(x,v)) | [fpf-val-single1] |
Def ma-sframe-compatible(A; B)
Def ==  kl:(Knd kl:(Knd IdLnk), tg:Id. IdLnk), tg:Id.
Def == ( kl kl  dom(1of(2of(2of(2of(2of(2of(A))))))) dom(1of(2of(2of(2of(2of(2of(A)))))))
Def == ( 
Def == ((tg  map( map( p.1of(p);1of(2of(2of(2of(2of(2of(A))))))(kl))) p.1of(p);1of(2of(2of(2of(2of(2of(A))))))(kl)))
Def == ( 
Def == (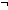  <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(A))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(A)))))))))
Def == ( 
Def == ( <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(B))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(B)))))))))
Def == ( 
Def == ( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of(
Def == ( deq-member(KindDeq;1of(kl);1of(B))))))))(<2of(kl),tg>))) deq-member(KindDeq;1of(kl);1of(B))))))))(<2of(kl),tg>)))
Def == & ( kl kl  dom(1of(2of(2of(2of(2of(2of(B))))))) dom(1of(2of(2of(2of(2of(2of(B)))))))
Def == & ( 
Def == & ((tg  map( map( p.1of(p);1of(2of(2of(2of(2of(2of(B))))))(kl))) p.1of(p);1of(2of(2of(2of(2of(2of(B))))))(kl)))
Def == & ( 
Def == & (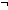  <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(B))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(B)))))))))
Def == & ( 
Def == & ( <2of(kl),tg> <2of(kl),tg>  dom(1of(2of(2of(2of(2of(2of(2of(2of(A))))))))) dom(1of(2of(2of(2of(2of(2of(2of(2of(A)))))))))
Def == & ( 
Def == & ( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of( deq-member(KindDeq;1of(kl);1of(2of(2of(2of(2of(2of(2of(2of(
Def == & ( deq-member(KindDeq;1of(kl);1of(A))))))))(<2of(kl),tg>))) deq-member(KindDeq;1of(kl);1of(A))))))))(<2of(kl),tg>))) | [ma-sframe-compatible] |
Def ma-frame-compatible(A; B)
Def ==  kx:(Knd kx:(Knd Id). Id).
Def == ( kx kx  dom(1of(2of(2of(2of(2of(A)))))) dom(1of(2of(2of(2of(2of(A))))))
Def == ( 
Def == (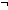  2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(A)))))))) dom(1of(2of(2of(2of(2of(2of(2of(A))))))))
Def == ( 
Def == ( 2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(B)))))))) dom(1of(2of(2of(2of(2of(2of(2of(B))))))))
Def == ( 
Def == ( deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of( deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of(
Def == ( deq-member(KindDeq;1of(kx);1of(B)))))))(2of(kx)))) deq-member(KindDeq;1of(kx);1of(B)))))))(2of(kx))))
Def == & ( kx kx  dom(1of(2of(2of(2of(2of(B)))))) dom(1of(2of(2of(2of(2of(B))))))
Def == & ( 
Def == & (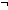  2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(B)))))))) dom(1of(2of(2of(2of(2of(2of(2of(B))))))))
Def == & ( 
Def == & ( 2of(kx) 2of(kx)  dom(1of(2of(2of(2of(2of(2of(2of(A)))))))) dom(1of(2of(2of(2of(2of(2of(2of(A))))))))
Def == & ( 
Def == & ( deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of( deq-member(KindDeq;1of(kx);1of(2of(2of(2of(2of(2of(2of(
Def == & ( deq-member(KindDeq;1of(kx);1of(A)))))))(2of(kx)))) deq-member(KindDeq;1of(kx);1of(A)))))))(2of(kx)))) | [ma-frame-compatible] |
Def Feasible(M)
Def ==  x x dom(1of(M)). T=1of(M)(x) dom(1of(M)). T=1of(M)(x)   T T
Def == &  k k dom(1of(2of(M))). T=1of(2of(M))(k) dom(1of(2of(M))). T=1of(2of(M))(k)   Dec(T) Dec(T)
Def == &  a a dom(1of(2of(2of(2of(M))))). p=1of(2of(2of(2of(M))))(a) dom(1of(2of(2of(2of(M))))). p=1of(2of(2of(2of(M))))(a)  
Def == & s:State(1of(M)). Dec( s:State(1of(M)). Dec(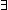 v:1of(2of(M))(locl(a))?Top. p(s,v)) v:1of(2of(M))(locl(a))?Top. p(s,v))
Def == &  kx kx dom(1of(2of(2of(2of(2of(M)))))). dom(1of(2of(2of(2of(2of(M)))))).
Def == ef=1of(2of(2of(2of(2of(M)))))(kx)   M.frame(1of(kx) affects 2of(kx)) M.frame(1of(kx) affects 2of(kx))
Def == &  kl kl dom(1of(2of(2of(2of(2of(2of(M))))))). dom(1of(2of(2of(2of(2of(2of(M))))))).
Def == & snd=1of(2of(2of(2of(2of(2of(M))))))(kl)    tg:Id. tg:Id.
Def == & (tg  map( map( p.1of(p);snd)) p.1of(p);snd))   M.sframe(1of(kl) sends <2of(kl),tg>) M.sframe(1of(kl) sends <2of(kl),tg>) | [ma-feasible] |
Def  x x dom(f). v=f(x) dom(f). v=f(x)   P(x;v) == P(x;v) ==  x:A. x:A.  x x  dom(f) dom(f)   P(x;f(x)) P(x;f(x)) | [fpf-all] |
Def f || g ==  x:A. x:A.  x x  dom(f) & dom(f) &  x x  dom(g) dom(g)   f(x) = g(x) f(x) = g(x)  B(x) B(x) | [fpf-compatible] |