| | Some definitions of interest. |
|
| ma-decla | Def a declared in M == 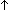 locl(a) locl(a)  dom(1of(2of(M))) dom(1of(2of(M))) |
|
| ma-npre | Def unsolvable M.pre(a,s)
Def == P != 1of(2of(2of(2of(M))))(a) ==>  v:M.da(locl(a)). v:M.da(locl(a)). 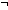 P(s,v) P(s,v) |
|
| ma-sub | Def M1 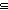 M2 M2
Def == 1of(M1) 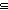 1of(M2) & 1of(2of(M1)) 1of(M2) & 1of(2of(M1)) 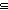 1of(2of(M2)) 1of(2of(M2))
Def == & 1of(2of(2of(M1))) 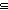 1of(2of(2of(M2))) 1of(2of(2of(M2)))
Def == & & 1of(2of(2of(2of(M1)))) 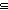 1of(2of(2of(2of(M2)))) 1of(2of(2of(2of(M2))))
Def == & & 1of(2of(2of(2of(2of(M1))))) 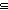 1of(2of(2of(2of(2of(M2))))) 1of(2of(2of(2of(2of(M2)))))
Def == & & 1of(2of(2of(2of(2of(2of(M1)))))) 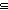 1of(2of(2of(2of(2of(2of(M2)))))) 1of(2of(2of(2of(2of(2of(M2))))))
Def == & & 1of(2of(2of(2of(2of(2of(2of(M1))))))) 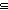 1of(2of(2of(2of(2of(2of(2of( 1of(2of(2of(2of(2of(2of(2of(
Def == & & 1of(2of(2of(2of(2of(2of(2of(M1)))))))  1of(M2))))))) 1of(M2)))))))
Def == & & 1of(2of(2of(2of(2of(2of(2of(2of(
Def == & & 1of(M1)))))))) 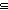 1of(2of(2of(2of(2of(2of(2of(2of(M2)))))))) 1of(2of(2of(2of(2of(2of(2of(2of(M2)))))))) |
|
| msga | Def MsgA
Def == ds:x:Id fp-> Type
Def ==  da:a:Knd fp-> Type da:a:Knd fp-> Type
Def ==  x:Id fp-> ds(x)?Void x:Id fp-> ds(x)?Void a:Id fp-> State(ds) a:Id fp-> State(ds)  ma-valtype(da; locl(a)) ma-valtype(da; locl(a))  Prop Prop
Def == kx:Knd Id fp-> State(ds) Id fp-> State(ds)  ma-valtype(da; 1of(kx)) ma-valtype(da; 1of(kx))  ds(2of(kx))?Void ds(2of(kx))?Void
Def == kl:Knd IdLnk fp-> (tg:Id IdLnk fp-> (tg:Id
Def == kl:Knd IdLnk fp-> ( IdLnk fp-> ( State(ds) State(ds)  ma-valtype(da; 1of(kl)) ma-valtype(da; 1of(kl)) 
Def == kl:Knd IdLnk fp-> ((da(rcv(2of(kl); tg))?Void List)) List IdLnk fp-> ((da(rcv(2of(kl); tg))?Void List)) List
Def ==  x:Id fp-> Knd List x:Id fp-> Knd List ltg:IdLnk ltg:IdLnk Id fp-> Knd List Id fp-> Knd List Top Top |
| | | Thm* MsgA  Type{i'} Type{i'} |
|
| Kind-deq | Def KindDeq == union-deq(IdLnk Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) Id;Id;product-deq(IdLnk;Id;IdLnkDeq;IdDeq);IdDeq) |
|
| ma-st | Def M.state == State(1of(M)) |
|
| Id | Def Id == Atom 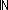 |
| | | Thm* Id  Type Type |
|
| fpf-cap | Def f(x)?z == if x  dom(f) dom(f)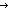 f(x) else z fi f(x) else z fi |
|
| locl | Def locl(a) == inr(a) |
| | | Thm*  a:Id. locl(a) a:Id. locl(a)  Knd Knd |
|
| top | Def Top == Void given Void |
| | | Thm* Top  Type Type |