| | Some definitions of interest. |
|
| d-feasible | Def d-feasible(D)
Def == ( i:Id. Feasible(M(i))) i:Id. Feasible(M(i)))
Def == & ( l:IdLnk, tg:Id. l:IdLnk, tg:Id.
Def == & (M(source(l)).dout(l,tg) 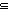 r M(destination(l)).din(l,tg)) r M(destination(l)).din(l,tg))
Def == & ( i:Id. i:Id.
Def == & (finite-type({l:IdLnk
Def == & (finite-type({| destination(l) = i & 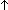 M(source(l)) sends on link l })) M(source(l)) sends on link l })) |
|
| interface-check | Def interface-check(D;l;tg;T) == T 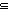 r M(destination(l)).din(l,tg) r M(destination(l)).din(l,tg) |
|
| ring-leader1 | Def ring-leader1(loc;R;uid;out;in)
Def == if R(loc)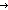
Def == if [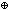 (send-once(loc; (send-once(loc; ; ; ;"send-me"; ;"send-me";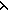 x.x;"vote";out(loc);"me")); x.x;"vote";out(loc);"me"));
Def == if [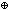 (trigger1(loc; (trigger1(loc; ; ; ; ;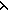 x,y. x= x,y. x=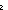 y;loc;rcv y;loc;rcv
Def == if [((in(loc)); "vote");"leader";"me"));
Def == if [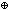 (Dconstant(loc; (Dconstant(loc; ;uid(loc);"me";loc)); ;uid(loc);"me";loc));
Def == if [ma-single-sends1( ; ;
Def == if [ma-single-sends1( ; ;
Def == if [ma-single-sends1( ; ;
Def == if [ma-single-sends1("me";
Def == if [ma-single-sends1(rcv((in(loc)); "vote");
Def == if [ma-single-sends1((out(loc));
Def == if [ma-single-sends1("vote";
Def == if [ma-single-sends1((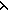 a,b. if a< a,b. if a<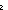 b b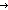 [b] else nil fi)); [b] else nil fi));
Def == if [only [rcv((in(loc)); "vote");
Def == if [only [locl("send-me")] sends on (out(loc) with "vote")]
Def == else nil fi |
|
| ma-join-list | Def 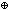 (L) == reduce( (L) == reduce(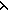 A,B. A A,B. A 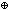 B;;L) B;;L) |
|
| ma-outlinks | Def ma-outlinks(M;i) == da-outlinks(1of(2of(M));i) |
|
| ring | Def ring(R;in;out)
Def == ( i:|R|. i:|R|.
Def == (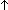 (R(source(in(i)))) & (R(source(in(i)))) & 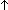 (R(destination(out(i)))) (R(destination(out(i))))
Def == (& source(out(i)) = i
Def == (& & destination(in(i)) = i
Def == (& & in(destination(out(i))) = out(i)  IdLnk IdLnk
Def == (& & out(source(in(i))) = in(i)  IdLnk) IdLnk)
Def == & ( i,j:|R|. i,j:|R|. 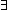 k: k: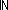 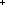 . . 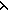 x.destination(out(x))^k(i) = j x.destination(out(x))^k(i) = j  Id) Id)
Def == & |R| |
| | | Thm*  R:(Id R:(Id  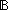 ), in,out:(|R| ), in,out:(|R|  IdLnk). ring(R;in;out) IdLnk). ring(R;in;out)  Prop Prop |
|
| IdLnk | Def IdLnk == Id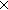 Id Id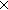 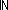 |
| | | Thm* IdLnk  Type Type |
|
| rset | Def |R| == {i:Id| 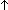 (R(i)) } (R(i)) } |
| | | Thm*  R:(Id R:(Id  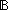 ). |R| ). |R|  Type Type |
|
| Id | Def Id == Atom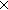 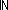 |
| | | Thm* Id  Type Type |
|
| assert | Def 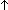 b == if b b == if b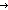 True else False fi True else False fi |
| | | Thm*  b: b: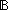 . b . b  Prop Prop |
|
| inject | Def Inj(A; B; f) ==  a1,a2:A. f(a1) = f(a2) a1,a2:A. f(a1) = f(a2)  B B 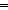  a1 = a2 a1 = a2 |
| | | Thm*  A,B:Type, f:(A A,B:Type, f:(A  B). Inj(A; B; f) B). Inj(A; B; f)  Prop Prop |
|
| l_all | Def ( x x L.P(x)) == L.P(x)) ==  x:T. (x x:T. (x  L) L) 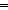  P(x) P(x) |
| | | Thm*  T:Type, L:T List, P:(T T:Type, L:T List, P:(T  Prop). ( Prop). ( x x L.P(x)) L.P(x))  Prop Prop |
|
| l_member | Def (x  l) == l) == 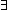 i: i: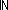 . i<||l|| & x = l[i] . i<||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |
|
| ldst | Def destination(l) == 1of(2of(l)) |
| | | Thm*  l:IdLnk. destination(l) l:IdLnk. destination(l)  Id Id |
|
| length | Def ||as|| == Case of as; nil 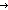 0 ; a.as' 0 ; a.as' 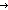 ||as'||+1 (recursive) ||as'||+1 (recursive) |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||   |
| | | Thm* ||nil||   |
|
| nat | Def 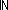 == {i: == {i: | 0 | 0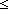 i } i } |
| | | Thm* 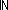  Type Type |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A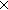 B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A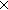 B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |