| | Who Cites spanner? |
|
| spanner | Def spanner(f;T;to;from)
Def == ( l:Edge(T). f(l) = l:Edge(T). f(l) = 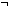 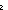 f(inverse(l))) f(inverse(l)))
Def == & ( i:|T|, l1,l2:Edge(T). i:|T|, l1,l2:Edge(T).
Def == & ((l1  to(i)) to(i))
Def == & (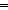 
Def == & ((l2  to(i)) to(i)) 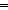  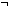 l1 = l2 l1 = l2  IdLnk IdLnk 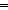  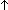 (f(l1)) (f(l1)) 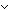 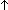 (f(l2))) (f(l2))) |
| | | Thm*  T:(Id T:(Id  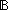 ), to,from:(|T| ), to,from:(|T|  (IdLnk List)), f:(Edge(T) (IdLnk List)), f:(Edge(T)  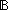 ). ).
Thm* bi-graph(T;to;from) 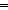  spanner(f;T;to;from) spanner(f;T;to;from)  Prop Prop |
|
| bi-graph-edge | Def Edge(G) == {l:IdLnk| 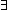 i:|G|. (l i:|G|. (l  from(i)) } from(i)) } |
|
| rset | Def |R| == {i:Id| 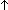 (R(i)) } (R(i)) } |
| | | Thm*  R:(Id R:(Id  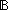 ). |R| ). |R|  Type Type |
|
| assert | Def 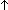 b == if b b == if b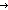 True else False fi True else False fi |
| | | Thm*  b: b: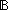 . b . b  Prop Prop |
|
| IdLnk | Def IdLnk == Id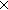 Id Id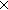 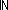 |
| | | Thm* IdLnk  Type Type |
|
| l_member | Def (x  l) == l) == 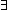 i: i: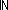 . i<||l|| & x = l[i] . i<||l|| & x = l[i]  T T |
| | | Thm*  T:Type, x:T, l:T List. (x T:Type, x:T, l:T List. (x  l) l)  Prop Prop |
|
| Id | Def Id == Atom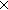 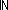 |
| | | Thm* Id  Type Type |
|
| nat | Def 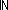 == {i: == {i: | 0 | 0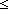 i } i } |
| | | Thm* 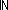  Type Type |
|
| le | Def A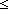 B == B == 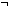 B<A B<A |
| | | Thm*  i,j: i,j: . (i . (i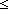 j) j)  Prop Prop |
|
| not | Def 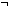 A == A A == A 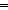  False False |
| | | Thm*  A:Prop. ( A:Prop. (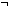 A) A)  Prop Prop |
|
| bi-graph-to | Def to(i) == to(i) |
|
| bi-graph-inv | Def inverse(l) == lnk-inv(l) |
|
| select | Def l[i] == hd(nth_tl(i;l)) |
| | | Thm*  A:Type, l:A List, n: A:Type, l:A List, n: . 0 . 0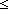 n n 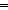  n<||l|| n<||l|| 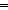  l[n] l[n]  A A |
|
| nth_tl | Def nth_tl(n;as) == if n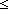 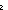 0 0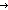 as else nth_tl(n-1;tl(as)) fi (recursive) as else nth_tl(n-1;tl(as)) fi (recursive) |
| | | Thm*  A:Type, as:A List, i: A:Type, as:A List, i: . nth_tl(i;as) . nth_tl(i;as)  A List A List |
|
| le_int | Def i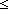 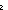 j == j == 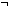 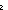 j< j<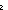 i i |
| | | Thm*  i,j: i,j: . (i . (i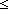 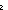 j) j)  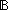 |
|
| bnot | Def 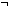 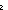 b == if b b == if b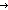 false false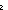 else true else true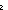 fi fi |
| | | Thm*  b: b: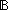 . . 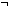 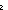 b b  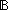 |
|
| length | Def ||as|| == Case of as; nil 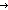 0 ; a.as' 0 ; a.as' 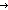 ||as'||+1 (recursive) ||as'||+1 (recursive) |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||   |
| | | Thm* ||nil||   |
|
| lnk-inv | Def lnk-inv(l) == <1of(2of(l)),1of(l),2of(2of(l))> |
|
| hd | Def hd(l) == Case of l; nil 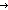 "?" ; h.t "?" ; h.t 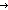 h h |
| | | Thm*  A:Type, l:A List. ||l|| A:Type, l:A List. ||l||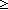 1 1 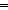  hd(l) hd(l)  A A |
|
| pi2 | Def 2of(t) == t.2 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A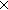 B(a)). 2of(p) B(a)). 2of(p)  B(1of(p)) B(1of(p)) |
|
| pi1 | Def 1of(t) == t.1 |
| | | Thm*  A:Type, B:(A A:Type, B:(A  Type), p:(a:A Type), p:(a:A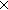 B(a)). 1of(p) B(a)). 1of(p)  A A |
|
| tl | Def tl(l) == Case of l; nil 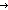 nil ; h.t nil ; h.t 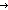 t t |
| | | Thm*  A:Type, l:A List. tl(l) A:Type, l:A List. tl(l)  A List A List |
|
| lt_int | Def i<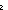 j == if i<j j == if i<j true true ; false ; false fi fi |
| | | Thm*  i,j: i,j: . (i< . (i< j) j)  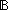 |