Nuprl - mb_hybrid LEMMAs for switch_inv_rel

Theorem	Name
Thm* E:TaggedEventStruct, tr:\|E\| List, ls:\|\|tr\|\|. switch_inv(E)(tr) (i,j:\|\|tr\|\|. (i (switchR(tr)^) ls) (j (switchR(tr)^) ls) tag(E)(tr[i]) = tag(E)(tr[j]))	[switch_inv_rel_closure]
cites
Thm* R,R2:(TTProp). Trans(T)(R2(_1,_2)) (x,y:T. (x R y) (x R2 y)) (x,y:T. (x (R^*) y) (x R2 y) x = y)	[rel_star_closure]
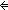Thm* E:TaggedEventStruct, tr:\|E\| List. switch_inv(E)(tr) (i,j:\|\|tr\|\|. (i switchR(tr) j) tag(E)(tr[i]) = tag(E)(tr[j]))	[switch_inv_rel_same_tag]