Selected Objects
| THM | no_dup_send_induced |  E:EventStruct, A:Type, evt:(A E:EventStruct, A:Type, evt:(A  |E|), tg:(A |E|), tg:(A  Label), tr_l:A List.
No-dup-send(E)(map(evt;tr_l)) Label), tr_l:A List.
No-dup-send(E)(map(evt;tr_l))   No-dup-send( < A,evt,tg > (E))(tr_l) No-dup-send( < A,evt,tg > (E))(tr_l) |
| def | remove_msgs | (L -msg(a;b) L1) == filter(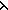 a.reduce( a.reduce(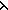 b,y. b,y.  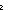 msg(a;b) msg(a;b) 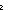 y;true y;true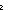 ;L1);L) ;L1);L) |
| THM | remove_msgs_nil |  msg:(A msg:(A  A A  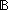 ), L1,L2:A List.
( ), L1,L2:A List.
( x:A. (x x:A. (x  L1) L1)   (x (x  L2)) L2))   Refl(A)(msg(_1,_2)) Refl(A)(msg(_1,_2))   (L1 -msg(a,b) L2) = nil (L1 -msg(a,b) L2) = nil |
| THM | remove_msgs_disjoint |  msg:(A msg:(A  A A  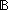 ), L1,L2:A List. ( ), L1,L2:A List. ( a,b:A. (a a,b:A. (a  L1) L1)   (b (b  L2) L2)    msg(a,b)) msg(a,b))   (L1 -msg(a,b) L2) = L1 (L1 -msg(a,b) L2) = L1 |
| def | switch_inv2001_03_15_DASH_PM_DASH_12_53_21 | switch_inv(E; tr)
==  i,j,k: i,j,k: ||tr||.
i < j ||tr||.
i < j   is-send(E)(tr[i])
is-send(E)(tr[i])   is-send(E)(tr[j])
is-send(E)(tr[j])  
 tag(E)(tr[i]) = tag(E)(tr[j]) tag(E)(tr[i]) = tag(E)(tr[j])   (tr[j] =msg=(E) tr[k])
(tr[j] =msg=(E) tr[k])  
 is-send(E)(tr[k]) is-send(E)(tr[k])   (
( k': k': ||tr||.
k' < k & loc(E)(tr[k']) = loc(E)(tr[k]) & (tr[i] =msg=(E) tr[k']) & ||tr||.
k' < k & loc(E)(tr[k']) = loc(E)(tr[k]) & (tr[i] =msg=(E) tr[k']) &  is-send(E)(tr[k'])) is-send(E)(tr[k'])) |
| def | deliveries_at | tr delivered at p == filter(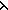 e. e. 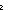 is-send(E)(e) is-send(E)(e) 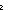 loc(E)(e) = loc(E)(e) = p;tr) p;tr) |
| def | delivered_at | x delivered at time k == (x =msg=(E) tr[k]) &  is-send(E)(tr[k]) is-send(E)(tr[k]) |
| def | P_tag_by_msg | Tag-by-msg(E)(tr) ==  i,j: i,j: ||tr||. (tr[i] =msg=(E) tr[j]) ||tr||. (tr[i] =msg=(E) tr[j])   tag(E)(tr[i]) = tag(E)(tr[j]) tag(E)(tr[i]) = tag(E)(tr[j]) |
| def | P_no_dup | No-dup-deliver(E)(tr)
==  i,j: i,j: ||tr||. ||tr||.
 is-send(E)(tr[i]) is-send(E)(tr[i])  
 is-send(E)(tr[j]) is-send(E)(tr[j])   (tr[j] =msg=(E) tr[i]) (tr[j] =msg=(E) tr[i])   loc(E)(tr[i]) = loc(E)(tr[j]) loc(E)(tr[i]) = loc(E)(tr[j])   i = j i = j |
| def | P_causal | Causal(E)(tr) ==  i: i: ||tr||. ||tr||.  j: j: ||tr||. j ||tr||. j i & is-send(E)(tr[j]) & (tr[j] =msg=(E) tr[i]) i & is-send(E)(tr[j]) & (tr[j] =msg=(E) tr[i]) |
| THM | P_causal_iff |  E:EventStruct, tr:|E| List.
Causal(E)(tr) E:EventStruct, tr:|E| List.
Causal(E)(tr) 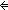  ( ( tr':|E| List. tr' tr':|E| List. tr'  tr tr   ( ( x x tr'.( tr'.( y y tr'.is-send(E)(y) & (y =msg=(E) x)))) tr'.is-send(E)(y) & (y =msg=(E) x)))) |
| THM | P_no_dup_iff |  E:EventStruct, tr:|E| List.
No-dup-deliver(E)(tr) E:EventStruct, tr:|E| List.
No-dup-deliver(E)(tr)
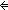  (
( x,y:|E|. x,y:|E|.
 is-send(E)(x) is-send(E)(x)  
 is-send(E)(y) is-send(E)(y)   (y =msg=(E) x) (y =msg=(E) x)   loc(E)(x) = loc(E)(y) loc(E)(x) = loc(E)(y)    sublist(|E|;[x; y];tr)) sublist(|E|;[x; y];tr)) |
| def | PTrue | PTrue(tr) == True |
| THM | P_tag_by_msg_lemma |  E:TaggedEventStruct, tr:|E| List.
( E:TaggedEventStruct, tr:|E| List.
( m:Label. Causal(E)( < tr > _m)) m:Label. Causal(E)( < tr > _m))   No-dup-send(E)(tr) No-dup-send(E)(tr)   Tag-by-msg(E)(tr) Tag-by-msg(E)(tr) |
| THM | P_causal_non_nil |  E:EventStruct, L:|E| List. E:EventStruct, L:|E| List.  L = nil L = nil   Causal(E)(L) Causal(E)(L)   ( ( i: i: ||L||. is-send(E)(L[i])) ||L||. is-send(E)(L[i])) |
| def | message_closure | C(Q)(i) ==  k: k: ||L||. Q(k) & (L[k] =msg=(E) L[i]) ||L||. Q(k) & (L[k] =msg=(E) L[i]) |
| def | single_tag_decomposable | single-tag-decomposable(E)(L)
==  L = nil L = nil  |E| List |E| List   (
( L_1,L_2:Trace(E).
L = (L_1 @ L_2) L_1,L_2:Trace(E).
L = (L_1 @ L_2)  |E| List
& |E| List
&  L_2 = nil L_2 = nil  |E| List
& ( |E| List
& ( x x L_1.( L_1.( y y L_2. L_2. (x =msg=(E) y)))
& ( (x =msg=(E) y)))
& ( m:Label. ( m:Label. ( x x L_2.tag(E)(x) = m))) L_2.tag(E)(x) = m))) |
| def | fusion_condition | I fuses P ==  tr:Trace(E). ( tr:Trace(E). ( m:Label. P( < tr > _m)) m:Label. P( < tr > _m))   I(tr) I(tr)   P(tr) P(tr) |
| THM | causal_fusion |  E:TaggedEventStruct. PTrue fuses Causal(E) E:TaggedEventStruct. PTrue fuses Causal(E) |
| def | R_ad_normal | R_ad_normal(tr)(a,b)
== (is-send(E)(a)    is-send(E)(b) is-send(E)(b)   (a =msg=(E) b))
& ( (a =msg=(E) b))
& ( is-send(E)(a) is-send(E)(a)  
 is-send(E)(b) is-send(E)(b)   (
( x,y: x,y: ||tr||.
x < y & is-send(E)(tr[x]) & is-send(E)(tr[y]) & (tr[x] =msg=(E) b) & (tr[y] =msg=(E) a)) ||tr||.
x < y & is-send(E)(tr[x]) & is-send(E)(tr[y]) & (tr[x] =msg=(E) b) & (tr[y] =msg=(E) a))
  loc(E)(a) = loc(E)(b))
loc(E)(a) = loc(E)(b)) |
| THM | decidable__R_ad_normal |  E:TaggedEventStruct, tr:|E| List, x,y:|E|. Dec(R_ad_normal(tr)(x,y)) E:TaggedEventStruct, tr:|E| List, x,y:|E|. Dec(R_ad_normal(tr)(x,y)) |
| def | R_composable | composableR(E)(L_1,L_2,L) == ( x x L_1.( L_1.( y y L_2. L_2. (x =msg=(E) y))) & L = (L_1 @ L_2) (x =msg=(E) y))) & L = (L_1 @ L_2)  |E| List |E| List |
| THM | P_no_dup_composable |  E:EventStruct. (ternary) composableR(E) preserves No-dup-deliver(E) E:EventStruct. (ternary) composableR(E) preserves No-dup-deliver(E) |
| def | R_strong_safety | Infix
R_strong_safety(E)(tr_1,tr_2) == sublist(|E|;tr_2;tr_1) |
| THM | P_no_dup_strong_safety |  E:EventStruct. R_strong_safety(E) preserves No-dup-deliver(E) E:EventStruct. R_strong_safety(E) preserves No-dup-deliver(E) |
| def | R_safety | Infix
safetyR(E)(tr_1,tr_2) == tr_2  tr_1 tr_1 |
| THM | no_duplicate_send_safety |  E:EventStruct. safetyR(E) preserves No-dup-send(E) E:EventStruct. safetyR(E) preserves No-dup-send(E) |
| THM | P_causal_safety |  E:EventStruct. safetyR(E) preserves Causal(E) E:EventStruct. safetyR(E) preserves Causal(E) |
| def | R_memoryless | Infix
memorylessR(E)(L_1,L_2) ==  a:|E|. L_2 = filter( a:|E|. L_2 = filter(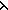 b. b. 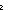 (b =msg=(E) a);L_1) (b =msg=(E) a);L_1)  |E| List |E| List |
| def | R_send_enabled | Infix
send-enabledR(E)(L_1,L_2) ==  x:|E|. is-send(E)(x) & L_2 = (L_1 @ [x]) x:|E|. is-send(E)(x) & L_2 = (L_1 @ [x]) |
| THM | P_no_dup_send_enabled |  E:EventStruct. send-enabledR(E) preserves No-dup-deliver(E) E:EventStruct. send-enabledR(E) preserves No-dup-deliver(E) |
| def | R_del | Macro
x R_del(E) y
==  (x =msg=(E) y) & is-deliver(E)(x) & is-send(E)(y) (x =msg=(E) y) & is-deliver(E)(x) & is-send(E)(y)  is-send(E)(x) & is-deliver(E)(y) is-send(E)(x) & is-deliver(E)(y) |
| def | tr_refines | P refines Q ==  tr:|E| List. P(tr) tr:|E| List. P(tr)   Q(tr) Q(tr) |
| THM | tr_refines_and |  E:Structure, P,Q_1,Q_2:((|E| List) E:Structure, P,Q_1,Q_2:((|E| List)  Prop).
(P refines Q_1) Prop).
(P refines Q_1)   (P refines Q_2) (P refines Q_2)   (P refines (Q_1 (P refines (Q_1  Q_2)) Q_2)) |
| def | trace_property | TraceProperty(E) == (|E| List)  Prop Prop |
| THM | fusion_weakening |  E:TaggedEventStruct, I,J,P:TraceProperty(E). (J refines I) E:TaggedEventStruct, I,J,P:TraceProperty(E). (J refines I)   (I fuses P) (I fuses P)   (J fuses P) (J fuses P) |
| THM | fusion_and |  E:TaggedEventStruct, I,P,Q:TraceProperty(E). (I fuses P) E:TaggedEventStruct, I,P,Q:TraceProperty(E). (I fuses P)   (I fuses Q) (I fuses Q)   (I fuses (P (I fuses (P  Q)) Q)) |
| THM | strong_safety_implies_safety |  E:EventStruct, P:TraceProperty(E). R_strong_safety(E) preserves P E:EventStruct, P:TraceProperty(E). R_strong_safety(E) preserves P   safetyR(E) preserves P safetyR(E) preserves P |
| THM | strong_safety_implies_memoryless |  E:EventStruct, P:TraceProperty(E). R_strong_safety(E) preserves P E:EventStruct, P:TraceProperty(E). R_strong_safety(E) preserves P   memorylessR(E) preserves P memorylessR(E) preserves P |
| THM | fusion_simplification |  E:TaggedEventStruct, I,J,P:TraceProperty(E).
((I E:TaggedEventStruct, I,J,P:TraceProperty(E).
((I  J) fuses P) J) fuses P)   (I fuses J) (I fuses J)   (P refines J) (P refines J)   (I fuses P) (I fuses P) |
| THM | memoryless_remove_msgs |  E:EventStruct, P:TraceProperty(E), L,L1:|E| List.
memorylessR(E) preserves P E:EventStruct, P:TraceProperty(E), L,L1:|E| List.
memorylessR(E) preserves P   P(L) P(L)   P((L -x =msg=(E) y L1)) P((L -x =msg=(E) y L1)) |
| def | swap_adjacent | Infix
swap adjacent[P(x;y)](L1,L2) ==  i: i: (||L1||-1). P(L1[i];L1[(i+1)]) & L2 = swap(L1;i;i+1) (||L1||-1). P(L1[i];L1[(i+1)]) & L2 = swap(L1;i;i+1)  A List A List |
| THM | normal_form_fusion |  E:TaggedEventStruct, P,I,J,K:TraceProperty(E), R:(Trace(E) E:TaggedEventStruct, P,I,J,K:TraceProperty(E), R:(Trace(E)  Trace(E) Trace(E)  Prop).
tag_splitable(E;R) Prop).
tag_splitable(E;R)   (
( tr_1,tr_2:Trace(E). (tr_1 R tr_2) tr_1,tr_2:Trace(E). (tr_1 R tr_2)   (tr_2 R tr_1)) (tr_2 R tr_1))   R preserves P
R preserves P   R preserves K
R preserves K   (
( tr:Trace(E). (I tr:Trace(E). (I  K)(tr) K)(tr)   ( ( tr':Trace(E). I(tr') & J(tr') & (tr R tr'))) tr':Trace(E). I(tr') & J(tr') & (tr R tr')))   (((I
(((I  J) J)  K) fuses P) K) fuses P)   ((I ((I  K) fuses P) K) fuses P) |
| THM | P_no_dup_deliver_safety |  E:EventStruct. safetyR(E) preserves No-dup-deliver(E) E:EventStruct. safetyR(E) preserves No-dup-deliver(E) |
| THM | P_tag_by_msg_safety |  E:TaggedEventStruct. safetyR(E) preserves Tag-by-msg(E) E:TaggedEventStruct. safetyR(E) preserves Tag-by-msg(E) |
| THM | tag_by_msg_fusion_lemma |  E:TaggedEventStruct, P,I:((|E| List) E:TaggedEventStruct, P,I:((|E| List)  Prop).
(P refines Causal(E)) Prop).
(P refines Causal(E))   ((I
((I  No-dup-send(E) No-dup-send(E)  Tag-by-msg(E)) fuses P) Tag-by-msg(E)) fuses P)   ((I ((I  No-dup-send(E)) fuses P) No-dup-send(E)) fuses P) |
| THM | no_dup_fusion |  E:TaggedEventStruct. Tag-by-msg(E) fuses No-dup-deliver(E) E:TaggedEventStruct. Tag-by-msg(E) fuses No-dup-deliver(E) |
| THM | no_DASH_dup_DASH_fusion |  E:TaggedEventStruct, P,I:((|E| List) E:TaggedEventStruct, P,I:((|E| List)  Prop).
(P refines (Causal(E) Prop).
(P refines (Causal(E)  No-dup-deliver(E))) No-dup-deliver(E)))   ((I
((I  No-dup-send(E) No-dup-send(E)  Tag-by-msg(E) Tag-by-msg(E)  Causal(E) Causal(E)  No-dup-deliver(E)) fuses P) No-dup-deliver(E)) fuses P)   ((I
((I  No-dup-send(E)) fuses P) No-dup-send(E)) fuses P) |
| def | tag_rel | R(tg) == swap adjacent[ tg(x) = tg(y) tg(x) = tg(y)  Label]^* Label]^* |
| def | totalorder | totalorder(E)(tr)
==  p,q:Label. agree_on_common(|MS(E)|;map(msg(E);tr delivered at p);map(msg(E);tr delivered at q)) p,q:Label. agree_on_common(|MS(E)|;map(msg(E);tr delivered at p);map(msg(E);tr delivered at q)) |
| THM | tag_sublist_preserved |  E:EventStruct, A:Type, evt:(A E:EventStruct, A:Type, evt:(A  |E|), tg:(A |E|), tg:(A  Label), m:Label, tr1,tr2:A List.
(tr1 R(tg) tr2) Label), m:Label, tr1,tr2:A List.
(tr1 R(tg) tr2)   < tr1 > _m = < tr2 > _m < tr1 > _m = < tr2 > _m  A List A List |
| def | local_deliver_property | local_deliver_property(E;P)(tr) == P(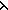 p.tr delivered at p) p.tr delivered at p) |
| def | delivered_before_somewhere | x somewhere delivered before y
==  k: k: ||tr||.
x delivered at time k
& ( ||tr||.
x delivered at time k
& ( k': k': ||tr||. y delivered at time k' ||tr||. y delivered at time k'   loc(E)(tr[k']) = loc(E)(tr[k]) loc(E)(tr[k']) = loc(E)(tr[k])   k k k') k') |
| THM | decidable__delivered_before_somewhere |  E:EventStruct, tr:|E| List, x,y:|E|. Dec(x somewhere delivered before y) E:EventStruct, tr:|E| List, x,y:|E|. Dec(x somewhere delivered before y) |
| def | switch_normal | AD-normal(E)(tr)
==  i: i: (||tr||-1).
(is-send(E)(tr[i]) (||tr||-1).
(is-send(E)(tr[i])    is-send(E)(tr[(i+1)]) is-send(E)(tr[(i+1)])   (tr[i] =msg=(E) tr[(i+1)]))
& (( (tr[i] =msg=(E) tr[(i+1)]))
& (( x,y: x,y: ||tr||.
x < y
& is-send(E)(tr[x])
& is-send(E)(tr[y])
& tr[x] delivered at time i+1
& tr[y] delivered at time i) ||tr||.
x < y
& is-send(E)(tr[x])
& is-send(E)(tr[y])
& tr[x] delivered at time i+1
& tr[y] delivered at time i)
  loc(E)(tr[i]) = loc(E)(tr[(i+1)]))
loc(E)(tr[i]) = loc(E)(tr[(i+1)])) |
| THM | not_delivered_before_somewhere |  E:EventStruct, a,b:|E|, tr:|E| List. E:EventStruct, a,b:|E|, tr:|E| List.
 a somewhere delivered before b a somewhere delivered before b
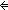  (
( k: k: ||tr||.
a delivered at time k ||tr||.
a delivered at time k   (
( k': k': ||tr||. k' < k & b delivered at time k' & loc(E)(tr[k']) = loc(E)(tr[k]))) ||tr||. k' < k & b delivered at time k' & loc(E)(tr[k']) = loc(E)(tr[k]))) |
| def | switch_decomposable | switch-decomposable(E)(L)
== L = nil  |E| List |E| List
 ( ( Q:( Q:( ||L|| ||L||  Prop).
( Prop).
( i: i: ||L||. Dec(Q(i)))
& ( ||L||. Dec(Q(i)))
& ( i: i: ||L||. Q(i))
& ( ||L||. Q(i))
& ( i: i: ||L||. Q(i) ||L||. Q(i)   is-send(E)(L[i]))
& ( is-send(E)(L[i]))
& ( i,j: i,j: ||L||. Q(i) ||L||. Q(i)   Q(j) Q(j)   tag(E)(L[i]) = tag(E)(L[j]))
& ( tag(E)(L[i]) = tag(E)(L[j]))
& ( i,j: i,j: ||L||. Q(i) ||L||. Q(i)   i i j j   C(Q)(j))) C(Q)(j))) |
| THM | switch_decomp_implies_single_tag_decomp |  E:TaggedEventStruct.
(switch-decomposable(E) E:TaggedEventStruct.
(switch-decomposable(E)  Tag-by-msg(E) Tag-by-msg(E)  Causal(E) Causal(E)  No-dup-send(E))
refines single-tag-decomposable(E) No-dup-send(E))
refines single-tag-decomposable(E) |
| THM | switch_normal_safety |  E:TaggedEventStruct. safetyR(E) preserves AD-normal(E) E:TaggedEventStruct. safetyR(E) preserves AD-normal(E) |
| THM | delivered_before_somewhere_lemma |  E:EventStruct, a,b,c:|E|, tr:|E| List.
a somewhere delivered before b E:EventStruct, a,b,c:|E|, tr:|E| List.
a somewhere delivered before b   a somewhere delivered before c a somewhere delivered before c  c somewhere delivered before b c somewhere delivered before b |
| def | memoryless_composable_safety | MCS(E)(P)
== memorylessR(E) preserves P & (ternary) composableR(E) preserves P & safetyR(E) preserves P |
| THM | M_DASH_C_DASH_S_SPACE_induction |  E:TaggedEventStruct, P,I:TraceProperty(E).
MCS(E)(P) E:TaggedEventStruct, P,I:TraceProperty(E).
MCS(E)(P)   safetyR(E) preserves I safetyR(E) preserves I   (I refines single-tag-decomposable(E)) (I refines single-tag-decomposable(E))   (I fuses P) (I fuses P) |
| def | R_permutation | R_permutation(E) == swap adjacent[True] |
| THM | P_no_dup_permutable |  E:EventStruct. R_permutation(E) preserves No-dup-deliver(E) E:EventStruct. R_permutation(E) preserves No-dup-deliver(E) |
| def | R_delayable | delayableR(E)
== swap adjacent[ (x =msg=(E) y) & (x =msg=(E) y) &  is-send(E)(x) & is-send(E)(y) is-send(E)(x) & is-send(E)(y)  is-send(E)(x) & is-send(E)(x) &  is-send(E)(y)] is-send(E)(y)] |
| THM | no_duplicate_send_delayable |  E:EventStruct. delayableR(E) preserves No-dup-send(E) E:EventStruct. delayableR(E) preserves No-dup-send(E) |
| THM | permutable_implies_delayable |  E:EventStruct, P:TraceProperty(E). R_permutation(E) preserves P E:EventStruct, P:TraceProperty(E). R_permutation(E) preserves P   delayableR(E) preserves P delayableR(E) preserves P |
| THM | R_delayable_symmetric |  E:EventStruct, x,y:|E| List. (x delayableR(E) y) E:EventStruct, x,y:|E| List. (x delayableR(E) y)   (y delayableR(E) x) (y delayableR(E) x) |
| def | R_async | asyncR(E)
== swap adjacent[ loc(E)(x) = loc(E)(y)
& loc(E)(x) = loc(E)(y)
&  is-send(E)(x) & is-send(E)(x) &  is-send(E)(y) is-send(E)(y)  is-send(E)(x) & is-send(E)(y)] is-send(E)(x) & is-send(E)(y)] |
| THM | no_duplicate_send_async |  E:EventStruct. asyncR(E) preserves No-dup-send(E) E:EventStruct. asyncR(E) preserves No-dup-send(E) |
| THM | permutable_implies_async |  E:EventStruct, P:TraceProperty(E). R_permutation(E) preserves P E:EventStruct, P:TraceProperty(E). R_permutation(E) preserves P   asyncR(E) preserves P asyncR(E) preserves P |
| THM | R_async_symmetric |  E:EventStruct, x,y:|E| List. (x asyncR(E) y) E:EventStruct, x,y:|E| List. (x asyncR(E) y)   (y asyncR(E) x) (y asyncR(E) x) |
| def | switch_inv | switch_inv(E)(tr)
==  i,j,k: i,j,k: ||tr||.
i < j ||tr||.
i < j   is-send(E)(tr[i])
is-send(E)(tr[i])   is-send(E)(tr[j])
is-send(E)(tr[j])  
 tag(E)(tr[i]) = tag(E)(tr[j]) tag(E)(tr[i]) = tag(E)(tr[j])   tr[j] delivered at time k
tr[j] delivered at time k   (
( k': k': ||tr||. k' < k & tr[i] delivered at time k' & loc(E)(tr[k']) = loc(E)(tr[k])) ||tr||. k' < k & tr[i] delivered at time k' & loc(E)(tr[k']) = loc(E)(tr[k])) |
| THM | switch_inv_swap |  E:TaggedEventStruct, x:|E| List, i: E:TaggedEventStruct, x:|E| List, i: (||x||-1).
switch_inv(E)(x) (||x||-1).
switch_inv(E)(x)  
 is-send(E)(x[(i+1)]) is-send(E)(x[(i+1)])   is-send(E)(x[i])
is-send(E)(x[i])   loc(E)(x[i]) = loc(E)(x[(i+1)]) loc(E)(x[i]) = loc(E)(x[(i+1)])   switch_inv(E)(swap(x;i;i+1)) switch_inv(E)(swap(x;i;i+1)) |
| THM | switch_inv_safety |  E:TaggedEventStruct. safetyR(E) preserves switch_inv(E) E:TaggedEventStruct. safetyR(E) preserves switch_inv(E) |
| def | layer_rel | layerR(E) == ((asyncR(E)  delayableR(E)) delayableR(E))  send-enabledR(E))^* send-enabledR(E))^* |
| THM | no_duplicate_send_layer |  E:EventStruct. layerR(E)^-1 preserves No-dup-send(E) E:EventStruct. layerR(E)^-1 preserves No-dup-send(E) |
| def | switch_inv_rel | Infix
switchR(tr)(i,j)
== is-send(E)(tr[i])
& is-send(E)(tr[j])
& i < j & tr[j] somewhere delivered before tr[i]  j < i & tr[i] somewhere delivered before tr[j] j < i & tr[i] somewhere delivered before tr[j] |
| THM | decidable__switch_inv_rel |  E:EventStruct, x:|E| List, j,z: E:EventStruct, x:|E| List, j,z: ||x||. Dec(j switchR(x) z) ||x||. Dec(j switchR(x) z) |
| def | switchable0 | switchable0(E)(P)
== safetyR(E) preserves P
& memorylessR(E) preserves P
& (ternary) composableR(E) preserves P
& send-enabledR(E) preserves P
& asyncR(E) preserves P
& delayableR(E) preserves P |
| THM | local_deliver_switchable |  E:EventStruct, P:((Label E:EventStruct, P:((Label  (|E| List)) (|E| List))  Prop).
( Prop).
( f,g:(Label f,g:(Label  (|E| List)). ( (|E| List)). ( p:Label. g(p) p:Label. g(p)  f(p)) f(p))   P(f) P(f)   P(g)) P(g))   (
( f,g:(Label f,g:(Label  (|E| List)).
( (|E| List)).
( a:|E|. a:|E|.  p:Label. g(p) = filter( p:Label. g(p) = filter(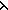 b. b. 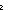 (b =msg=(E) a);f(p))) (b =msg=(E) a);f(p)))   P(f) P(f)   P(g)) P(g))
  (
( f,g,h:(Label f,g,h:(Label  (|E| List)).
( (|E| List)).
( p,q:Label. ( p,q:Label. ( x x f(p).( f(p).( y y g(q). g(q). (x =msg=(E) y)))) (x =msg=(E) y))))   (
( p:Label. h(p) = ((f(p)) @ (g(p)))) p:Label. h(p) = ((f(p)) @ (g(p))))   P(f) P(f)   P(g) P(g)   P(h)) P(h))
  switchable0(E)(local_deliver_property(E;P))
switchable0(E)(local_deliver_property(E;P)) |
| THM | P_causal_switchable0 |  E:EventStruct. switchable0(E)(Causal(E)) E:EventStruct. switchable0(E)(Causal(E)) |
| THM | P_no_dup_switchable0 |  E:EventStruct. switchable0(E)(No-dup-deliver(E)) E:EventStruct. switchable0(E)(No-dup-deliver(E)) |
| THM | switch_inv_rel_closure_send |  E:EventStruct, tr:|E| List, ls,i: E:EventStruct, tr:|E| List, ls,i: ||tr||.
is-send(E)(tr[ls]) ||tr||.
is-send(E)(tr[ls])   (i (switchR(tr)^*) ls) (i (switchR(tr)^*) ls)   is-send(E)(tr[i]) is-send(E)(tr[i]) |
| THM | switch_inv_rel_same_tag |  E:TaggedEventStruct, tr:|E| List.
switch_inv(E)(tr) E:TaggedEventStruct, tr:|E| List.
switch_inv(E)(tr) 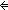  ( ( i,j: i,j: ||tr||. (i switchR(tr) j) ||tr||. (i switchR(tr) j)   tag(E)(tr[i]) = tag(E)(tr[j])) tag(E)(tr[i]) = tag(E)(tr[j])) |
| def | b_switchable | switchable(E)(P)
== safetyR(E) preserves P
& memorylessR(E) preserves P
& (ternary) composableR(E) preserves P
& send-enabledR(E) preserves P
& asyncR(E) preserves P
& delayableR(E) preserves P
& (P refines Causal(E))
& (P refines No-dup-deliver(E)) |
| THM | totalorder_switchable0 |  E:EventStruct. switchable0(E)(totalorder(E)) E:EventStruct. switchable0(E)(totalorder(E)) |
| THM | switchable0_switchable |  E:EventStruct, P:TraceProperty(E).
switchable0(E)(P) E:EventStruct, P:TraceProperty(E).
switchable0(E)(P)   switchable(E)(P switchable(E)(P  Causal(E) Causal(E)  No-dup-deliver(E)) No-dup-deliver(E)) |
| THM | switch_inv_rel_closure |  E:TaggedEventStruct, tr:|E| List, ls: E:TaggedEventStruct, tr:|E| List, ls: ||tr||.
switch_inv(E)(tr) ||tr||.
switch_inv(E)(tr)   (
( i,j: i,j: ||tr||. (i (switchR(tr)^*) ls) ||tr||. (i (switchR(tr)^*) ls)   (j (switchR(tr)^*) ls) (j (switchR(tr)^*) ls)   tag(E)(tr[i]) = tag(E)(tr[j])) tag(E)(tr[i]) = tag(E)(tr[j])) |
| THM | switch_inv_rel_closure_lemma1 |  E:EventStruct, tr:|E| List, ls: E:EventStruct, tr:|E| List, ls: ||tr||.
is-send(E)(tr[ls]) ||tr||.
is-send(E)(tr[ls])   (
( j: j: ||tr||. ls < j ||tr||. ls < j    is-send(E)(tr[j])) is-send(E)(tr[j]))   (
( i,j: i,j: ||tr||. i ||tr||. i j j   is-send(E)(tr[j]) is-send(E)(tr[j])   (i (switchR(tr)^*) ls) (i (switchR(tr)^*) ls)   (j (switchR(tr)^*) ls)) (j (switchR(tr)^*) ls)) |
| def | R_ad | adR(E) == (delayableR(E)  asyncR(E))^* asyncR(E))^* |
| THM | tag_sublist_layer |  E:TaggedEventStruct. tag_splitable(E;adR(E)) E:TaggedEventStruct. tag_splitable(E;adR(E)) |
| THM | switchable_induced |  E:EventStruct, A:Type, f:(A E:EventStruct, A:Type, f:(A  |E|), P:((|E| List) |E|), P:((|E| List)  Prop).
switchable(E)(P) Prop).
switchable(E)(P)   switchable(induced_event_str(E;A;f))(P o f) switchable(induced_event_str(E;A;f))(P o f) |
| THM | totalorder_switchable |  E:EventStruct. switchable(E)(totalorder(E) E:EventStruct. switchable(E)(totalorder(E)  Causal(E) Causal(E)  No-dup-deliver(E)) No-dup-deliver(E)) |
| THM | strong_switch_inv_decomposable |  E:TaggedEventStruct.
(switch_inv(E) E:TaggedEventStruct.
(switch_inv(E)  Causal(E) Causal(E)  AD-normal(E) AD-normal(E)  No-dup-deliver(E)) refines switch-decomposable(E) No-dup-deliver(E)) refines switch-decomposable(E) |
| def | full_switch_inv | full_switch_inv(E;A;evt;tg;tr_u;tr_l)
==  tr_m:A List.
(tr_l R(tg) tr_m) & (map(evt;tr_m) layerR(E) tr_u) & switch_inv( < A,evt,tg > (E))(tr_m) tr_m:A List.
(tr_l R(tg) tr_m) & (map(evt;tr_m) layerR(E) tr_u) & switch_inv( < A,evt,tg > (E))(tr_m) |
| THM | switch_normal_exists |  E:TaggedEventStruct, tr:Trace(E).
(switch_inv(E) E:TaggedEventStruct, tr:Trace(E).
(switch_inv(E)  No-dup-send(E))(tr) No-dup-send(E))(tr)   (
( tr':Trace(E). switch_inv(E)(tr') & AD-normal(E)(tr') & (tr adR(E) tr')) tr':Trace(E). switch_inv(E)(tr') & AD-normal(E)(tr') & (tr adR(E) tr')) |
| THM | switchable_induced_tagged |  E:EventStruct, P:((|E| List) E:EventStruct, P:((|E| List)  Prop), A:Type, f:(A Prop), A:Type, f:(A  |E|), t:(A |E|), t:(A  Label).
switchable(E)(P) Label).
switchable(E)(P)   switchable( < A,f,t > (E))(P o f) switchable( < A,f,t > (E))(P o f) |
| THM | switch_inv_plus_normal |  E:TaggedEventStruct, P:TraceProperty(E).
MCS(E)(P) E:TaggedEventStruct, P:TraceProperty(E).
MCS(E)(P)   (P refines (Causal(E)
(P refines (Causal(E)  No-dup-deliver(E))) No-dup-deliver(E)))   (((switch_inv(E)
(((switch_inv(E)  AD-normal(E)) AD-normal(E))  No-dup-send(E)) fuses P) No-dup-send(E)) fuses P) |
| THM | switch_inv_theorem |  E:TaggedEventStruct, P:TraceProperty(E).
MCS(E)(P) E:TaggedEventStruct, P:TraceProperty(E).
MCS(E)(P)   asyncR(E) preserves P
asyncR(E) preserves P   delayableR(E) preserves P
delayableR(E) preserves P   (P refines (Causal(E)
(P refines (Causal(E)  No-dup-deliver(E))) No-dup-deliver(E)))   ((switch_inv(E) ((switch_inv(E)  No-dup-send(E)) fuses P) No-dup-send(E)) fuses P) |
| THM | switch_inv_theorem2 |  E:TaggedEventStruct, P:TraceProperty(E).
switchable(E)(P) E:TaggedEventStruct, P:TraceProperty(E).
switchable(E)(P)   ((switch_inv(E) ((switch_inv(E)  No-dup-send(E)) fuses P) No-dup-send(E)) fuses P) |
| THM | switch_theorem |  E:EventStruct, P:((|E| List) E:EventStruct, P:((|E| List)  Prop), A:Type, evt:(A Prop), A:Type, evt:(A  |E|), tg:(A |E|), tg:(A  Label), tr:A List.
switchable(E)(P) Label), tr:A List.
switchable(E)(P)   No-dup-send(E)(map(evt;tr))
No-dup-send(E)(map(evt;tr))   switch_inv( < A,evt,tg > (E))(tr)
switch_inv( < A,evt,tg > (E))(tr)   ( ( m:Label. P(map(evt; < tr > _m))) m:Label. P(map(evt; < tr > _m)))   P(map(evt;tr)) P(map(evt;tr)) |
| THM | switch_main_theorem |  E:EventStruct, P:TraceProperty(E), A:Type, evt:(A E:EventStruct, P:TraceProperty(E), A:Type, evt:(A  |E|), tg:(A |E|), tg:(A  Label), tr_u:Trace(E), tr_l:A List.
switchable(E)(P) Label), tr_u:Trace(E), tr_l:A List.
switchable(E)(P)   No-dup-send(E)(tr_u)
No-dup-send(E)(tr_u)   full_switch_inv(E;A;evt;tg;tr_u;tr_l)
full_switch_inv(E;A;evt;tg;tr_u;tr_l)   ( ( m:Label. P(map(evt; < tr_l > _m))) m:Label. P(map(evt; < tr_l > _m)))   P(tr_u) P(tr_u) |