| Rank | Theorem | Name |
| 7 | Thm*  i: i: , L:A List. , L:A List.
Thm* i+1<||L||
Thm*  
Thm* ( X,Y:A List. X,Y:A List.
Thm* (L = (X @ [L[i]; L[(i+1)]] @ Y)
Thm* (& swap(L;i;i+1) = (X @ [L[(i+1)]; L[i]] @ Y)) | [swap_adjacent_decomp] |
| cites the following: |
| 1 | Thm*  a,b:T List. ||a|| = ||b|| a,b:T List. ||a|| = ||b||     ( ( i: i: . i<||a|| . i<||a||   a[i] = b[i]) a[i] = b[i])   a = b a = b | [list_extensionality] |
| 3 | Thm*  L:T List, i,j: L:T List, i,j: ||L||. ||swap(L;i;j)|| = ||L|| ||L||. ||swap(L;i;j)|| = ||L||   | [swap_length] |
| 6 | Thm*  L1,L2:T List, i,j: L1,L2:T List, i,j: ||L1||. ||L1||.
Thm* L2 = swap(L1;i;j)
Thm*  
Thm* L2[i] = L1[j] & L2[j] = L1[i] & ||L2|| = ||L1||   & L1 = swap(L2;i;j) & L1 = swap(L2;i;j)
Thm* & ( x: x: ||L2||. ||L2||.  x = i x = i    x = j x = j   L2[x] = L1[x]) L2[x] = L1[x]) | [swapped_select] |
| 0 | Thm*  a:T, as:T List, i: a:T, as:T List, i: . 0<i . 0<i   i i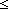 ||as|| ||as||   [a / as][i] = as[(i-1)] [a / as][i] = as[(i-1)] | [select_cons_tl] |
| 0 | Thm*  l:A List. ||l|| l:A List. ||l||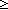 1 1   ||tl(l)|| = ||l||-1 ||tl(l)|| = ||l||-1   | [length_tl] |
| 5 | Thm*  L:T List, x:T, i,j:{1..(||L||+1) L:T List, x:T, i,j:{1..(||L||+1) }. }.
Thm* swap([x / L];i;j) = [x / swap(L;i-1;j-1)] | [swap_cons] |
| 1 | Thm*  as:A List, n: as:A List, n: (||as||-1). tl(as)[n] = as[(n+1)] (||as||-1). tl(as)[n] = as[(n+1)] | [select_tl] |