| equiv_rel |
Def EquivRel x,y:T. E(x;y)
== Refl(T;x,y.E(x;y)) & Sym x,y:T. E(x;y) & Trans x,y:T. E(x;y)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). (EquivRel x,y:T. E(x,y)) Prop). (EquivRel x,y:T. E(x,y)) 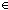 Prop Prop
|
| lang_rel |
Def L-induced Equiv(x,y) ==  z:A*. L(z @ x) z:A*. L(z @ x)   L(z @ y) L(z @ y)
Thm*  A:Type, L:LangOver(A). L-induced Equiv A:Type, L:LangOver(A). L-induced Equiv 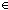 A* A*  A* A*  Prop Prop
|
| languages |
Def LangOver(Alph) == Alph*  Prop Prop
Thm*  Alph:Type{i}. LangOver(Alph) Alph:Type{i}. LangOver(Alph) 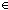 Type{i'} Type{i'}
|
| refl |
Def Refl(T;x,y.E(x;y)) ==  a:T. E(a;a) a:T. E(a;a)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Refl(T;x,y.E(x,y)) Prop). Refl(T;x,y.E(x,y)) 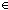 Prop Prop
|
| sym |
Def Sym x,y:T. E(x;y) ==  a,b:T. E(a;b) a,b:T. E(a;b)   E(b;a) E(b;a)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Sym x,y:T. E(x,y) Prop). Sym x,y:T. E(x,y) 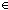 Prop Prop
|
| trans |
Def Trans x,y:T. E(x;y) ==  a,b,c:T. E(a;b) a,b,c:T. E(a;b)   E(b;c) E(b;c)   E(a;c) E(a;c)
Thm*  T:Type, E:(T T:Type, E:(T  T T  Prop). Trans x,y:T. E(x,y) Prop). Trans x,y:T. E(x,y) 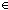 Prop Prop
|
| append |
Def as @ bs == Case of as; nil 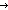 bs ; a.as' bs ; a.as' 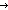 a.(as' @ bs) (recursive) a.(as' @ bs) (recursive)
Thm*  T:Type, as,bs:T*. (as @ bs) T:Type, as,bs:T*. (as @ bs) 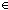 T* T*
|
| iff |
Def P   Q == (P Q == (P   Q) & (P Q) & (P   Q) Q)
Thm*  A,B:Prop. (A A,B:Prop. (A   B) B) 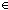 Prop Prop
|
| rev_implies |
Def P   Q == Q Q == Q   P P
Thm*  A,B:Prop. (A A,B:Prop. (A   B) B) 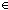 Prop Prop
|
![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). (EquivRel x,y:T. E(x,y))
Prop). (EquivRel x,y:T. E(x,y)) ![]() Prop
Prop![]() A:Type, L:LangOver(A). L-induced Equiv
A:Type, L:LangOver(A). L-induced Equiv ![]() A*
A*![]()
![]() A*
A*![]()
![]() Prop
Prop![]() Alph:Type{i}. LangOver(Alph)
Alph:Type{i}. LangOver(Alph) ![]() Type{i'}
Type{i'}![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). Refl(T;x,y.E(x,y))
Prop). Refl(T;x,y.E(x,y)) ![]() Prop
Prop![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). Sym x,y:T. E(x,y)
Prop). Sym x,y:T. E(x,y) ![]() Prop
Prop![]() T:Type, E:(T
T:Type, E:(T![]()
![]() T
T![]()
![]() Prop). Trans x,y:T. E(x,y)
Prop). Trans x,y:T. E(x,y) ![]() Prop
Prop![]() T:Type, as,bs:T*. (as @ bs)
T:Type, as,bs:T*. (as @ bs) ![]() T*
T*![]() A,B:Prop. (A
A,B:Prop. (A ![]()
![]() B)
B) ![]() Prop
Prop![]() A,B:Prop. (A
A,B:Prop. (A ![]()
![]() B)
B) ![]() Prop
Prop