| 1 | 18. BL: S.car*
19.  t:S.car. mem_f(S.car;t;BL) t:S.car. mem_f(S.car;t;BL)   ( ( a:Alph. S.act(a,t) = u) a:Alph. S.act(a,t) = u)
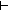  AL:S.car*.
( AL:S.car*.
( s:S.car. mem_f(S.car;s;AL) s:S.car. mem_f(S.car;s;AL)   ( ( w:Alph*. mem_f(S.car;(S:w w:Alph*. mem_f(S.car;(S:w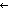 s);sL)))
& ( s);sL)))
& ( s:S.car. mem_f(S.car;s;sL) s:S.car. mem_f(S.car;s;sL)   u = s u = s 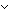 mem_f(S.car;s;TBL) mem_f(S.car;s;TBL) 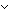 mem_f(S.car;s;AL))
& ( mem_f(S.car;s;AL))
& ( s:S.car, a:Alph.
u = S.act(a,s) s:S.car, a:Alph.
u = S.act(a,s) 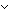 mem_f(S.car;S.act(a,s);TBL) mem_f(S.car;S.act(a,s);TBL)   u = s u = s 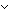 mem_f(S.car;s;TBL) mem_f(S.car;s;TBL) 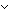 mem_f(S.car;s;AL)) mem_f(S.car;s;AL)) |