At: total back listify 1 2 1 2 2 1
1. Alph: Type
2. S: ActionSet(Alph)
3. sL: S.car*
4. Fin(Alph)
5. n: 
6. f:  n
n
 S.car
S.car
7. g: S.car

 n
n
8. InvFuns( n; S.car; f; g)
n; S.car; f; g)
9.  n:
n: .
.
 TBL:S.car*.
(
TBL:S.car*.
( s:S.car. mem_f(S.car;s;TBL)
s:S.car. mem_f(S.car;s;TBL) 
 (
( w:Alph*. mem_f(S.car;(S:w
w:Alph*. mem_f(S.car;(S:w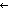 s);sL)))
s);sL)))
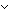 ||TBL|| = n
& (
||TBL|| = n
& ( i:
i: ||TBL||, j:
||TBL||, j: i.
i.  TBL[i] = TBL[j])
& (
TBL[i] = TBL[j])
& ( s:S.car. mem_f(S.car;s;TBL)
s:S.car. mem_f(S.car;s;TBL) 
 (
( w:Alph*. mem_f(S.car;(S:w
w:Alph*. mem_f(S.car;(S:w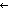 s);sL)))
& (
s);sL)))
& ( AL:S.car*.
(
AL:S.car*.
( s:S.car. mem_f(S.car;s;AL)
s:S.car. mem_f(S.car;s;AL) 
 (
( w:Alph*. mem_f(S.car;(S:w
w:Alph*. mem_f(S.car;(S:w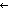 s);sL)))
& (
s);sL)))
& ( s:S.car. mem_f(S.car;s;sL)
s:S.car. mem_f(S.car;s;sL) 
 mem_f(S.car;s;TBL)
mem_f(S.car;s;TBL) 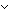 mem_f(S.car;s;AL))
& (
mem_f(S.car;s;AL))
& ( s:S.car, a:Alph. mem_f(S.car;S.act(a,s);TBL)
s:S.car, a:Alph. mem_f(S.car;S.act(a,s);TBL) 
 mem_f(S.car;s;TBL)
mem_f(S.car;s;TBL) 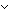 mem_f(S.car;s;AL)))
mem_f(S.car;s;AL)))
10.  n = 0
n = 0
11. TBL: S.car*
12. ||TBL|| = n+1 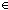

13.  i:
i: ||TBL||, j:
||TBL||, j: i.
i.  TBL[i] = TBL[j]
TBL[i] = TBL[j]
14.  s:S.car. mem_f(S.car;s;TBL)
s:S.car. mem_f(S.car;s;TBL) 
 (
( w:Alph*. mem_f(S.car;(S:w
w:Alph*. mem_f(S.car;(S:w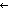 s);sL))
s);sL))
15. AL: S.car*
16.  s:S.car. mem_f(S.car;s;AL)
s:S.car. mem_f(S.car;s;AL) 
 (
( w:Alph*. mem_f(S.car;(S:w
w:Alph*. mem_f(S.car;(S:w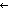 s);sL))
s);sL))
17.  s:S.car. mem_f(S.car;s;sL)
s:S.car. mem_f(S.car;s;sL) 
 mem_f(S.car;s;TBL)
mem_f(S.car;s;TBL) 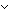 mem_f(S.car;s;AL)
mem_f(S.car;s;AL)
18.  s:S.car, a:Alph. mem_f(S.car;S.act(a,s);TBL)
s:S.car, a:Alph. mem_f(S.car;S.act(a,s);TBL) 
 mem_f(S.car;s;TBL)
mem_f(S.car;s;TBL) 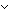 mem_f(S.car;s;AL)
mem_f(S.car;s;AL)
19. i:  (n+1)
(n+1)
20. j:  i
i
21. g(TBL[i]) = g(TBL[j])
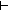
 TBL:S.car*.
TBL:S.car*.  s:S.car. mem_f(S.car;s;TBL)
s:S.car. mem_f(S.car;s;TBL) 
 (
( w:Alph*. mem_f(S.car;(S:w
w:Alph*. mem_f(S.car;(S:w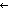 s);sL))
s);sL))
By:
InstHyp [i;j] 13
THEN
Analyze -1
Generated subgoal:| 1 | 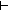 TBL[i] = TBL[j] TBL[i] = TBL[j] |
About: