Selected Objects
| THM | length_reverse |  l:T*. ||rev(l)|| = ||l|| l:T*. ||rev(l)|| = ||l|| 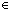  |
| THM | hd_select |  l:T*. ||l|| > 0 l:T*. ||l|| > 0 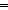  hd(l) = l[0] hd(l) = l[0] |
| THM | hd_append_front |  l,m:T*. ||l|| > 0 l,m:T*. ||l|| > 0 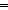  hd((l @ m)) = hd(l) hd((l @ m)) = hd(l) |
| THM | hd_append_back |  l,m:T*. ||l|| = 0 l,m:T*. ||l|| = 0 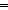  ||m|| > 0 ||m|| > 0 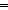  hd((l @ m)) = hd(m) hd((l @ m)) = hd(m) |
| THM | hd_map |  l:A*, f:(A l:A*, f:(A 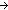 B). ||l|| > 0 B). ||l|| > 0 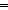  hd(map(f;l)) = f(hd(l)) hd(map(f;l)) = f(hd(l)) |
| THM | tl_append_front |  l,m:T*. ||l|| > 0 l,m:T*. ||l|| > 0 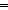  tl((l @ m)) = (tl(l) @ m) tl((l @ m)) = (tl(l) @ m) |
| THM | tl_append_back |  l,m:T*. ||l|| = 0 l,m:T*. ||l|| = 0 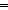  ||m|| > 0 ||m|| > 0 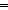  tl((l @ m)) = tl(m) tl((l @ m)) = tl(m) |
| THM | reverse_cons_nil |  t:T. rev([t]) = [t] t:T. rev([t]) = [t] |
| THM | hd_reverse |  l:T*. ||l|| > 0 l:T*. ||l|| > 0 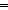  hd(rev(l)) = l[(||l||-1)] hd(rev(l)) = l[(||l||-1)] |
| def | nd_automata | NDA(Alph;States) == (States 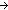 Alph Alph 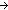 States States 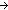 Prop) Prop) States States (States (States 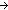 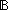 ) ) |
| def | NDA_act | 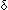 n == 1of(n) n == 1of(n) |
| def | NDA_init | I(n) == 1of(2of(n)) |
| def | NDA_fin | F(n) == 2of(2of(n)) |
| def | cook_nd_automata | NDA(act;init;fin) == < act,init,fin > |
| def | nd_compute_list | (rec) NDA(l)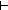 q == if null(l) q == if null(l) q = I(NDA) q = I(NDA) 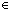 St else St else  t:St. NDA(tl(l)) t:St. NDA(tl(l))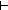 t & t & 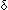 NDA(t,hd(l),q) fi NDA(t,hd(l),q) fi |
| def | nd_accept_list | NDA(l)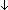 == ==  q:St. NDA(l) q:St. NDA(l)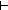 q & F(NDA)(q) q & F(NDA)(q) |
| def | nd_auto_lang | L(NDA)(l) == NDA(l)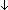 |
| THM | nd_auto_eq_auto |  NDA:NDA(Alph;St).
Fin(St) NDA:NDA(Alph;St).
Fin(St) 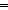  (
( x,y:St, a:Alph. Dec( x,y:St, a:Alph. Dec(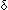 NDA(x,a,y))) NDA(x,a,y))) 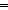  (
( S:Type. Fin(S) & ( S:Type. Fin(S) & ( DA:Automata(Alph;S). L(NDA) = LangOf(DA))) DA:Automata(Alph;S). L(NDA) = LangOf(DA))) |
| def | nd_computation | NComp(Alph;St) == {C:(St Alph* List Alph* List )| )|  i: i: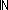 (||C||-1). ||2of(C[i])|| > 0 } (||C||-1). ||2of(C[i])|| > 0 } |
| def | nd_comp_car | |C| == 2of(hd(C)) |
| def | nd_comp_length | ||C|| == ||C|| |
| def | nd_comp_init | [ < q,[] > ] == [ < q,nil > ] |
| THM | nd_comp_init_thm |  NDA:NDA(Alph;St). NDA([ < I(NDA),[] > ]) NDA:NDA(Alph;St). NDA([ < I(NDA),[] > ])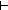 I(NDA) I(NDA) |
| def | nd_comp_extend | C+[a;q] == map( c. < 1of(c),a.2of(c) > ;C) @ [ < q,nil > ] c. < 1of(c),a.2of(c) > ;C) @ [ < q,nil > ] |
| def | nd_valcom | NDA(C)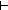 q
== I(NDA) = 1of(hd(C)) q
== I(NDA) = 1of(hd(C)) 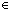 St
& ( St
& ( i: i: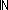 (||C||-1). (||C||-1).
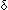 NDA(1of(C[i]),hd(rev(2of(C[i]))),1of(C[(i+1)]))
& 2of(C[(i+1)]) = rev(tl(rev(2of(C[i])))) NDA(1of(C[i]),hd(rev(2of(C[i]))),1of(C[(i+1)]))
& 2of(C[(i+1)]) = rev(tl(rev(2of(C[i])))) 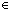 Alph*)
& 1of(hd(rev(C))) = q Alph*)
& 1of(hd(rev(C))) = q 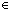 St
& 2of(hd(rev(C))) = nil St
& 2of(hd(rev(C))) = nil 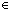 Alph* Alph* |
| THM | nd_init_valcom |  NDA:NDA(Alph;St). NDA([ < I(NDA),[] > ]) NDA:NDA(Alph;St). NDA([ < I(NDA),[] > ])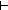 I(NDA) I(NDA) |
| THM | nd_ext_valcom |  NDA:NDA(Alph;St), C:NComp(Alph;St), q:St, a:Alph, p:St. NDA(C) NDA:NDA(Alph;St), C:NComp(Alph;St), q:St, a:Alph, p:St. NDA(C)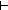 q q 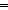  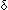 NDA(q,a,p) NDA(q,a,p) 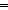  NDA(C+[a;p]) NDA(C+[a;p])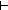 p p |