| 1 | 11. 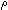 ( < x1.(M @ N),concl > ) < ( < x1.(M @ N),concl > ) < 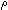 ( < M @ (x1 ( < M @ (x1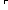 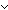 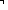 x2.N),concl > ) x2.N),concl > ) 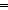 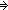 (
(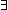 L:Sequent List. L:Sequent List.
 s s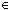 L.( L.(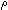 (s) = 0)
& ( (s) = 0)
& ( s s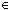 L.|= s L.|= s 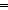 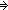 |= < x1.(M @ N),concl > )
& ( |= < x1.(M @ N),concl > )
& ( a:Assignment. a:Assignment. 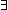 s s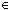 L.a | L.a |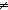 s s 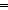 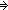 a | a |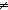 < x1.(M @ N),concl > )) < x1.(M @ N),concl > ))
12. 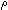 ( < x2.(M @ N),concl > ) < ( < x2.(M @ N),concl > ) < 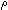 ( < M @ (x1 ( < M @ (x1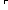 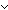 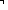 x2.N),concl > ) x2.N),concl > ) 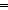 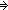 (
(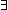 L:Sequent List. L:Sequent List.
 s s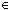 L.( L.(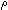 (s) = 0)
& ( (s) = 0)
& ( s s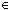 L.|= s L.|= s 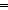 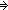 |= < x2.(M @ N),concl > )
& ( |= < x2.(M @ N),concl > )
& ( a:Assignment. a:Assignment. 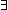 s s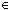 L.a | L.a |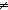 s s 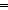  a | a | < x2.(M @ N),concl > )) < x2.(M @ N),concl > ))
  L:Sequent List. L:Sequent List.
 s s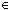 L.( L.(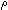 (s) = 0)
& ( (s) = 0)
& ( s s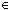 L.|= s L.|= s 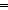 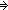 |= < M @ (x1 |= < M @ (x1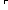 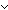 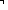 x2.N),concl > )
& ( x2.N),concl > )
& ( a:Assignment. a:Assignment. 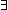 s s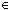 L.a | L.a |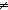 s s 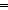  a | a | < M @ (x1 < M @ (x1  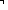 x2.N),concl > ) x2.N),concl > ) |