| valuation |
Def (F under a)
== (letrec val f = case f:
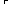 x x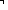  (a(x)); (a(x));
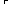 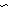 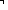 p p  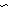  val(p);
p val(p);
p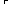 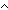 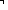 q q  val(p) val(p) 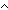  val(q);
p val(q);
p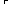 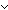 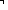 q q  val(p) val(p) 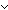  val(q);
p val(q);
p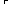 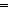 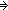 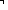 q q  val(p) val(p) 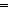 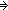  val(q); )
(F) val(q); )
(F)
Thm*  a:Assignment, F:Formula. (F under a) a:Assignment, F:Formula. (F under a) 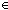 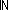 
|
| K_imp |
Def p 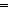 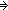  q == case p: 3 q == case p: 3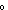  3 3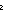 ; 3 ; 3  case q: 3 case q: 3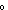  3 3 ; 3 ; 3  3 3 ; 3 ; 3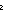  3 3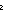 ;; 3 ;; 3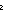  q; q;
Thm*  p,q: p,q: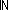  . p . p 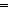 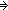  q q 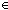 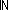 
|
| K_or |
Def p 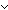  q == case p: 3 q == case p: 3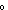  q; 3 q; 3  case q: 3 case q: 3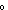  3 3 ; 3 ; 3  3 3 ; 3 ; 3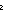  3 3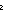 ;; 3 ;; 3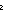  3 3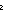 ; ;
Thm*  p,q: p,q: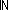  . p . p   q q 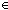 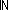 
|
| K_and |
Def p 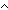  q == case p: 3 q == case p: 3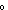  3 3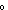 ; 3 ; 3  case q: 3 case q: 3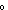  3 3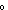 ; 3 ; 3  3 3 ; 3 ; 3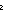  3 3 ;; 3 ;; 3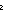  q; q;
Thm*  p,q: p,q: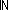  . p . p 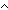  q q 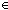 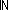 
|
| K_not |
Def 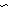  p == case p: 3 p == case p: 3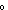  3 3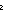 ; 3 ; 3  3 3 ; 3 ; 3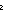  3 3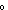 ; ;
Thm*  p: p: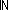  . . 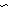  p p 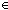 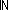 
|
| formula_case |
Def case F:
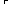 x x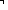  varC(x); varC(x);
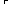 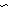 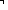 p1 p1  notC(p1);
p2 notC(p1);
p2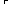 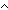 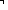 p3 p3  andC(p2;p3);
p4 andC(p2;p3);
p4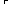 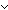 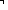 p5 p5  orC(p4;p5);
p6 orC(p4;p5);
p6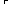 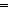 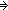  p7 p7  impC(p6;p7);
== InjCase(F; x. varC(x); F.
InjCase(F; p1. notC(p1); F.
InjCase(F; x. x/p2,p3.andC(p2;p3); F. InjCase(F; x. x/p4,p5.orC(p4;p5), x/p6,p7.impC(p6;p7))))) impC(p6;p7);
== InjCase(F; x. varC(x); F.
InjCase(F; p1. notC(p1); F.
InjCase(F; x. x/p2,p3.andC(p2;p3); F. InjCase(F; x. x/p4,p5.orC(p4;p5), x/p6,p7.impC(p6;p7)))))
|
| letrec_body |
Def = b == b
|
| letrec_arg |
Def x b(x) (x) == b(x)
|
| letrec |
Def (letrec f b(f)) == b((letrec f b(f)) ) (recursive)
|
| Three_1 |
Def 3 == inr(inl( == inr(inl( )) ))
Thm* 3 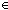 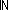 
|
| Three_2 |
Def 3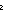 == inr(inr( == inr(inr(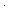 )) ))
Thm* 3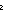 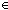 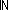 
|
| Three_case |
Def case x: 3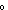  case0; 3 case0; 3  case1; 3 case1; 3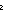  case2;
== InjCase(x; zero. case0; one_or_two. InjCase(one_or_two; one. case1; two. case2)) case2;
== InjCase(x; zero. case0; one_or_two. InjCase(one_or_two; one. case1; two. case2))
Thm*  t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3 t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3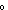 : 3 : 3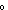  c; 3 c; 3  c'; 3 c'; 3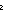  c''; c''; 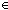 t t
Thm*  t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3 t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3 : 3 : 3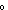  c'; 3 c'; 3  c''; 3 c''; 3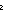  c; c; 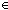 t'' t''
Thm*  t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3 t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3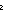 : 3 : 3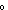  c; 3 c; 3  c'; 3 c'; 3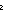  c''; c''; 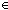 t'' t''
|
| Three_0 |
Def 3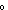 == inl( == inl(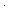 ) )
Thm* 3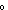 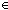 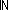 
|
![]() a:Assignment, F:Formula. (F under a)
a:Assignment, F:Formula. (F under a) ![]()
![]()
![]()
![]() p,q:
p,q:![]()
![]() . p
. p ![]()
![]()
![]() q
q ![]()
![]()
![]()
![]() p,q:
p,q:![]()
![]() . p
. p ![]()
![]() q
q ![]()
![]()
![]()
![]() p,q:
p,q:![]()
![]() . p
. p ![]()
![]() q
q ![]()
![]()
![]()
![]() p:
p:![]()
![]() .
. ![]()
![]() p
p ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3
t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3![]() : 3
: 3![]()
![]() c; 3
c; 3![]()
![]() c'; 3
c'; 3![]()
![]() c'';
c''; ![]() t
t
![]() t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3
t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3![]() : 3
: 3![]()
![]() c'; 3
c'; 3![]()
![]() c''; 3
c''; 3![]()
![]() c;
c; ![]() t''
t''
![]() t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3
t:Type{i}, t':Type{j}, t'':Type{k}, c:t, c':t', c'':t''.
case 3![]() : 3
: 3![]()
![]() c; 3
c; 3![]()
![]() c'; 3
c'; 3![]()
![]() c'';
c''; ![]() t''
t''![]()
![]()
![]()
![]()