| C |
Def s.C == s.2
Thm*  s:Sequent. s.C s:Sequent. s.C 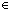 Formula List Formula List
|
| Sequent |
Def Sequent == (Formula List)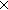 (Formula List) (Formula List)
Thm* Sequent 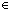 Type Type
|
| Formula |
Def Formula
== rec(formula.Var+formula+(formula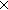 formula)+(formula formula)+(formula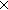 formula)+(formula formula)+(formula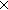 formula)) formula))
Thm* Formula 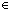 Type Type
|
| H |
Def s.H == s.1
Thm*  s:Sequent. s.H s:Sequent. s.H 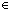 Formula List Formula List
|
| list_rank |
Def 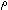 (L) == reduce( (L) == reduce(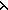 x,y. x,y. 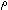 (x)+y;0;L) (x)+y;0;L)
Thm* 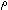 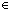 (Formula List) (Formula List) 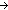 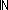
|
| nat |
Def 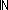 == {i: == {i: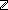 | 0 | 0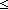 i } i }
Thm* 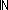 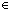 Type Type
|
| Var |
Def Var == Atom
Thm* Var 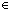 Type Type
|
| formula_rank |
Def 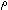 == (letrec formula_rank f = case f:
== (letrec formula_rank f = case f:
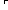 x x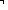 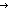 0; 0;
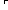 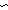 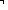 p p 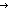 (formula_rank(p)+1);
p (formula_rank(p)+1);
p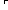 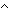 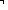 q q 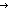 (formula_rank(p)+formula_rank(q)+1);
p (formula_rank(p)+formula_rank(q)+1);
p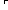 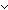 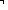 q q 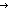 (formula_rank(p)+formula_rank(q)+1);
p (formula_rank(p)+formula_rank(q)+1);
p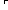 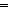 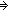 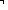 q q 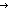 (formula_rank(p)+formula_rank(q)+1); ) (formula_rank(p)+formula_rank(q)+1); )
Thm* 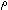 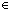 Formula Formula 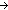 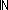
|
| reduce |
Def reduce(f;k;as) == Case of as; nil 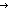 k ; a.as' k ; a.as' 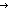 f(a,reduce(f;k;as')) (recursive) f(a,reduce(f;k;as')) (recursive)
Thm*  A,B:Type, f:(A A,B:Type, f:(A 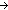 B B 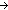 B), k:B, as:A List. reduce(f;k;as) B), k:B, as:A List. reduce(f;k;as) 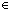 B B
|
| le |
Def A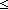 B == B == 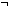 B < A B < A
Thm*  i,j: i,j: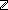 . i . i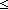 j j 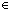 Prop Prop
|
| formula_case |
Def case F:
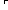 x x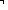 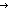 varC(x); varC(x);
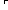 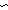 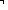 p1 p1 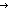 notC(p1);
p2 notC(p1);
p2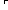 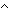 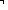 p3 p3 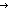 andC(p2;p3);
p4 andC(p2;p3);
p4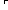 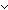 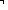 p5 p5 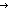 orC(p4;p5);
p6 orC(p4;p5);
p6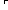 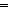 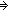 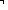 p7 p7 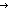 impC(p6;p7);
== InjCase(F; x. varC(x); F.
InjCase(F; p1. notC(p1); F.
InjCase(F; x. x/p2,p3.andC(p2;p3); F. InjCase(F; x. x/p4,p5.orC(p4;p5), x/p6,p7.impC(p6;p7))))) impC(p6;p7);
== InjCase(F; x. varC(x); F.
InjCase(F; p1. notC(p1); F.
InjCase(F; x. x/p2,p3.andC(p2;p3); F. InjCase(F; x. x/p4,p5.orC(p4;p5), x/p6,p7.impC(p6;p7)))))
|
| letrec_body |
Def = b == b
|
| letrec_arg |
Def x b(x) (x) == b(x)
|
| letrec |
Def (letrec f b(f)) == b((letrec f b(f)) ) (recursive)
|
| not |
Def 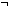 A == A A == A 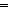 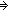 False False
Thm*  A:Prop. ( A:Prop. (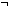 A) A) 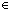 Prop Prop
|
![]() s:Sequent. s.C
s:Sequent. s.C ![]() Formula List
Formula List![]() Type
Type![]() Type
Type![]() s:Sequent. s.H
s:Sequent. s.H ![]() Formula List
Formula List![]()
![]() (Formula List)
(Formula List)![]()
![]()
![]()
![]()
![]() Type
Type![]() Type
Type![]()
![]() Formula
Formula![]()
![]()
![]()
![]() A,B:Type, f:(A
A,B:Type, f:(A![]()
![]() B
B![]()
![]() B), k:B, as:A List. reduce(f;k;as)
B), k:B, as:A List. reduce(f;k;as) ![]() B
B![]() i,j:
i,j:![]() . i
. i![]() j
j ![]() Prop
Prop![]() A:Prop. (
A:Prop. (![]() A)
A) ![]() Prop
Prop