---

Step * 1 of Lemma aa_max_ltree_spec3


1. t : aa_ltree()@i
2. aa_binary_search_tree(t)@i
3. i : @i
4. aa_bst_member_prop(i;t)@i
5. aa_max_ltree(t) = (inr  )@i
 False
BY
{ ((RepUR ``aa_max_ltree`` 5 THEN RecUnfold `aa_ltree_ind` 5 THEN DVar `t'  THEN MoveToHyp 0 5 THEN HypSubst' 6 7)
   THEN DVar `t1' THEN Reduce 7 THEN MaAuto
   ) }

1
1. t : rec(X.Unit + (val: 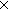 left_subtree:X  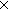X))
2. aa_binary_search_tree(t)@i
3. i : @i
4. aa_bst_member_prop(i;t)@i
5. x : Unit
6. t = (inl x )
7. (inr  ) = (inr  )
 False

2
1. t : rec(X.Unit + (val: 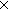 left_subtree:X  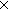X))
2. aa_binary_search_tree(t)@i
3. i : @i
4. aa_bst_member_prop(i;t)@i
5. y : val: 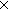 left_subtree:aa_ltree()  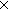aa_ltree()
6. t = (inr y )
7. aa_max_w_unit(inl (fst(y)) ;aa_ltree_ind(snd(snd(y));inr  ;val,left_subtree,right_subtree,rec1,rec2....))
= (inr  )
 False



1.  t  :  aa\_ltree(\mBbbZ{})@i
2.  aa\_binary\_search\_tree(t)@i
3.  i  :  \mBbbZ{}@i
4.  aa\_bst\_member\_prop(i;t)@i
5.  aa\_max\_ltree(t)  =  (inr  \mcdot{}  )@i
\mvdash{}  False


By

((RepUR  ``aa\_max\_ltree``  5  THEN  RecUnfold  `aa\_ltree\_ind`  5  THEN  DVar  `t'    THEN  MoveToHyp  0  5
    THEN  HypSubst'  6  7
    )
  THEN  DVar  `t1'  THEN  Reduce  7  THEN  MaAuto
  )



Home Index