Nuprl Lemma : ross_pnp
 P:
P: . (P
. (P 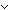 (
( P) //True
P) //True 
 (P //True
(P //True 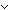
 P //True))
P //True))
Proof
Definitions occuring in Statement :
prop:  ,
all:
,
all:  x:A. B[x],
not:
x:A. B[x],
not:  A,
implies: P
A,
implies: P 
 Q,
or: P
Q,
or: P 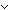 Q,
true: True,
quotient: x,y:A//B[x; y]
Q,
true: True,
quotient: x,y:A//B[x; y]
Definitions :
so_lambda: 
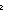 x y.t[x; y],
member: t
x y.t[x; y],
member: t  T,
trans: Trans(T;x,y.E[x; y]),
sym: Sym(T;x,y.E[x; y]),
refl: Refl(T;x,y.E[x; y]),
and: P
T,
trans: Trans(T;x,y.E[x; y]),
sym: Sym(T;x,y.E[x; y]),
refl: Refl(T;x,y.E[x; y]),
and: P  Q,
equiv_rel: EquivRel(T;x,y.E[x; y]),
true: True,
or: P
Q,
equiv_rel: EquivRel(T;x,y.E[x; y]),
true: True,
or: P 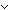 Q,
implies: P
Q,
implies: P 
 Q,
prop:
Q,
prop:  ,
all:
,
all:  x:A. B[x],
squash:
x:A. B[x],
squash:  T,
so_apply: x[s1;s2],
uimplies: b supposing a,
uall:
T,
so_apply: x[s1;s2],
uimplies: b supposing a,
uall:  [x:A]. B[x],
false: False,
not:
[x:A]. B[x],
false: False,
not:  A
A
Lemmas :
not_wf,
or_wf,
quotient_wf,
true_wf,
inr_wf,
squash_wf,
inl_wf
\mforall{}P:\mBbbP{}. (P \mvee{} (\mneg{}P) //True {}\mRightarrow{} (P //True \mvee{} \mneg{}P //True))
Date html generated:
2013_03_20-AM-09_51_44
Last ObjectModification:
2012_11_27-AM-10_32_10
Home
Index