Step
*
1
1
1
2
of Lemma
gcd_sq_exists_anne
1. n :  @i
@i
2.  n1:
n1: n.
n.  m:
m: . (
. (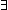 g:{
g:{ | GCD(m;n1;g)})@i
| GCD(m;n1;g)})@i
3. m :  @i
@i
4. 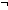 (n = 0)
(n = 0)
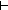
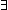 g:{
g:{ | GCD(m;n;g)}
| GCD(m;n;g)}
BY
{ (InstHyp [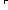 m rem n
m rem n ;
;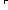 n
n ] 2
] 2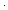 THENA Auto) }
THENA Auto) }
1
1. n :  @i
@i
2.  n1:
n1: n.
n.  m:
m: . (
. (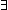 g:{
g:{ | GCD(m;n1;g)})@i
| GCD(m;n1;g)})@i
3. m :  @i
@i
4. 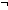 (n = 0)
(n = 0)
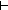 (m rem n) < n
(m rem n) < n
2
1. n :  @i
@i
2.  n1:
n1: n.
n.  m:
m: . (
. (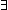 g:{
g:{ | GCD(m;n1;g)})@i
| GCD(m;n1;g)})@i
3. m :  @i
@i
4. 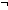 (n = 0)
(n = 0)
5. 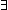 g:{
g:{ | GCD(n;m rem n;g)}
| GCD(n;m rem n;g)}
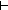
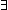 g:{
g:{ | GCD(m;n;g)}
| GCD(m;n;g)}
1. n : \mBbbN{}@i
2. \mforall{}n1:\mBbbN{}n. \mforall{}m:\mBbbN{}. (\mexists{}g:\{\mBbbN{}| GCD(m;n1;g)\})@i
3. m : \mBbbN{}@i
4. \mneg{}(n = 0)
\mvdash{} \mexists{}g:\{\mBbbN{}| GCD(m;n;g)\}
By
(InstHyp [\mkleeneopen{}m rem n\mkleeneclose{};\mkleeneopen{}n\mkleeneclose{}] 2\mcdot{} THENA Auto)
Home
Index