Step
*
2
1
1
of Lemma
maxsegsum_singleton
1. x : 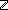 @i
@i
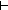 (
(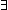 h:
h: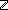 .
. 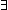 t:
t: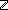 List. ([x] = [h / t]))
List. ([x] = [h / t]))
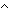 (
( r:
r: ||[x]||. (x
||[x]||. (x 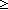 initseg_sum(r;[x]) ))
initseg_sum(r;[x]) ))
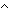 (
(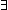 c:
c: ||[x]||. (x = initseg_sum(c;[x])))
||[x]||. (x = initseg_sum(c;[x])))
BY
{ D 0 }
1
1. x : 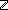 @i
@i
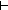
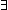 h:
h: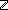 .
. 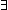 t:
t: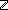 List. ([x] = [h / t])
List. ([x] = [h / t])
2
1. x : 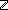 @i
@i
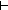 (
( r:
r: ||[x]||. (x
||[x]||. (x 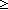 initseg_sum(r;[x]) ))
initseg_sum(r;[x]) )) 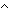 (
(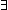 c:
c: ||[x]||. (x = initseg_sum(c;[x])))
||[x]||. (x = initseg_sum(c;[x])))
Latex:
1. x : \mBbbZ{}@i
\mvdash{} (\mexists{}h:\mBbbZ{}. \mexists{}t:\mBbbZ{} List. ([x] = [h / t]))
\mwedge{} (\mforall{}r:\mBbbN{}||[x]||. (x \mgeq{} initseg\_sum(r;[x]) ))
\mwedge{} (\mexists{}c:\mBbbN{}||[x]||. (x = initseg\_sum(c;[x])))
By
D 0
Home
Index