Nuprl Lemma : dataflow-bags-equiv

{

[A,B:Type].

[b1,b2:bag(dataflow(A;bag(B)))].
(dataflow-bags-equiv(A;B;b1;b2)

) }

{ Proof }

Definitions occuring in Statement : dataflow-bags-equiv: dataflow-bags-equiv(A;B;b1;b2), dataflow: dataflow(A;B), uall:

[x:A]. B[x], prop:

, member: t

T, universe: Type, bag: bag(T)
Definitions : length: ||as||, add: n + m, true: True, le: A

B, ge: i

j , subtype: S

T, top: Top, sqequal: s ~ t, null: null(as), corec: corec(T.F[T]), quotient: x,y:A//B[x; y], strong-subtype: strong-subtype(A;B), l_member: (x

l), less_than: a < b, product: x:A

B[x], and: P

Q, uiff: uiff(P;Q), subtype_rel: A

r B, assert:

b, void: Void, implies: P

Q, false: False, not:

A, set: {x:A| B[x]} , list: type List, data-stream: data-stream(P;L), uimplies: b supposing a, last: last(L), lambda:

x.A[x], so_lambda:

x.t[x], bag-combine:

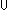x

bs.f[x], limited-type: LimitedType, listp: A List

, function: x:A

B[x], all:

x:A. B[x], uall:

[x:A]. B[x], dataflow: dataflow(A;B), isect:

x:A. B[x], axiom: Ax, prop:

, universe: Type, dataflow-bags-equiv: dataflow-bags-equiv(A;B;b1;b2), member: t

T, equal: s = t, bag: bag(T), Auto: Error :Auto, CollapseTHEN: Error :CollapseTHEN, D: Error :D
Lemmas : false_wf, assert_wf, not_wf, top_wf, member_wf, null-data-stream, pos_length2, bag_wf, data-stream_wf, last_wf, dataflow_wf, bag-combine_wf, listp_wf, listp_properties, true_wf

\mforall{}[A,B:Type]. \mforall{}[b1,b2:bag(dataflow(A;bag(B)))]. (dataflow-bags-equiv(A;B;b1;b2) \mmember{} \mBbbP{}) Date html generated: 2011_08_16-AM-09_48_47 Last ObjectModification: 2011_04_27-PM-03_40_42 Home Index