{  [A:
[A: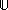 '].
'].  [B:Type].
[B:Type].  [x:dataflow(A;bag(B))]. is-null-df(x)
[x:dataflow(A;bag(B))]. is-null-df(x) 
 supposing
supposing  A }
A }
{ Proof }
Definitions occuring in Statement :
is-null-df: is-null-df(x),
dataflow: dataflow(A;B),
bool:  ,
uimplies: b supposing a,
uall:
,
uimplies: b supposing a,
uall:  [x:A]. B[x],
squash:
[x:A]. B[x],
squash:  T,
member: t
T,
member: t  T,
universe: Type,
bag: bag(T)
T,
universe: Type,
bag: bag(T)
Definitions :
atom: Atom$n,
int:  ,
atom: Atom,
rec: rec(x.A[x]),
quotient: x,y:A//B[x; y],
tunion:
,
atom: Atom,
rec: rec(x.A[x]),
quotient: x,y:A//B[x; y],
tunion: 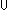 x:A.B[x],
b-union: A
x:A.B[x],
b-union: A 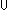 B,
implies: P
B,
implies: P 
 Q,
list: type List,
union: left + right,
strong-subtype: strong-subtype(A;B),
le: A
Q,
list: type List,
union: left + right,
strong-subtype: strong-subtype(A;B),
le: A  B,
ge: i
B,
ge: i  j ,
not:
j ,
not:  A,
less_than: a < b,
product: x:A
A,
less_than: a < b,
product: x:A  B[x],
and: P
B[x],
and: P  Q,
uiff: uiff(P;Q),
subtype_rel: A
Q,
uiff: uiff(P;Q),
subtype_rel: A  r B,
valueall-type: valueall-type(T),
null-dataflow: null-dataflow(),
eq_term: a == b,
set: {x:A| B[x]} ,
bnot:
r B,
valueall-type: valueall-type(T),
null-dataflow: null-dataflow(),
eq_term: a == b,
set: {x:A| B[x]} ,
bnot: 
 b,
bfalse: ff,
btrue: tt,
function: x:A
b,
bfalse: ff,
btrue: tt,
function: x:A 
 B[x],
all:
B[x],
all:  x:A. B[x],
primrec: primrec(n;b;c),
corec: corec(T.F[T]),
axiom: Ax,
uall:
x:A. B[x],
primrec: primrec(n;b;c),
corec: corec(T.F[T]),
axiom: Ax,
uall:  [x:A]. B[x],
bag: bag(T),
dataflow: dataflow(A;B),
uimplies: b supposing a,
universe: Type,
prop:
[x:A]. B[x],
bag: bag(T),
dataflow: dataflow(A;B),
uimplies: b supposing a,
universe: Type,
prop:  ,
squash:
,
squash:  T,
isect:
T,
isect:  x:A. B[x],
member: t
x:A. B[x],
member: t  T,
equal: s = t,
bool:
T,
equal: s = t,
bool:  ,
is-null-df: is-null-df(x)
,
is-null-df: is-null-df(x)
Lemmas :
valueall-type_wf,
dataflow_wf,
bag_wf,
null-dataflow_wf,
eq_term_wf,
squash_wf,
dataflow-valueall-type
\mforall{}[A:\mBbbU{}']. \mforall{}[B:Type]. \mforall{}[x:dataflow(A;bag(B))]. is-null-df(x) \mmember{} \mBbbB{} supposing \mdownarrow{}A
Date html generated:
2011_08_16-AM-09_48_04
Last ObjectModification:
2011_02_03-PM-01_27_36
Home
Index