| | Some definitions of interest. |
|
| complete_intseg_mset | Def complete_intseg_mset(a; b; f)(x) == if a 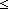 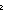 x < x <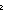 b b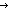 f(x) else 0 fi f(x) else 0 fi |
| | | Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ). complete_intseg_mset(a; b; f) ). complete_intseg_mset(a; b; f) 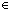     |
|
| prime_factorization_of | Def f is a factorization of k
Def == ( x:Prime x:Prime . k<x . k<x   f(x) = 0) & k = f(x) = 0) & k =   {2..k+1 {2..k+1 }(prime_mset_complete(f)) }(prime_mset_complete(f)) |
| | | Thm*  f:(Prime f:(Prime    ), k: ), k: . f is a factorization of k . f is a factorization of k 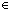 Prop Prop |
|
| eval_factorization | Def   {a..b {a..b }(f) == }(f) ==  i:{a..b i:{a..b }. i }. i f(i) f(i) |
| | | Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ). ).   {a..b {a..b }(f) }(f) 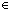  |
|
| is_prime_factorization | Def is_prime_factorization(a; b; f) ==  i:{a..b i:{a..b }. 0<f(i) }. 0<f(i)   prime(i) prime(i) |
| | | Thm*  a,b: a,b: , f:({a..b , f:({a..b } }   ). is_prime_factorization(a; b; f) ). is_prime_factorization(a; b; f) 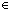 Prop Prop |
|
| int_seg | Def {i..j } == {k: } == {k: | i | i 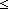 k < j } k < j } |
| | | Thm*  m,n: m,n: . {m..n . {m..n } } 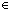 Type Type |
|
| int_upper | Def {i...} == {j: | i | i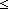 j } j } |
| | | Thm*  n: n: . {n...} . {n...} 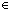 Type Type |
|
| prime_nats | Def Prime == {x: == {x: | prime(x) } | prime(x) } |
|
| nat | Def  == {i: == {i: | 0 | 0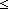 i } i } |
| | | Thm*  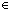 Type Type |
|
| prime_mset_complete | Def prime_mset_complete(f)(x) == if is_prime(x)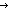 f(x) else 0 fi f(x) else 0 fi |
| | | Thm*  f:(Prime f:(Prime    ). prime_mset_complete(f) ). prime_mset_complete(f) 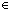     |