| | Some definitions of interest. |
|
| prime_nats | Def Prime == {x: == {x: | prime(x) } | prime(x) } |
|
| nat | Def  == {i: == {i: | 0 | 0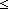 i } i } |
| | | Thm*  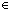 Type Type |
|
| prime | Def prime(a) == 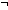 a = 0 & a = 0 & 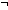 (a ~ 1) & ( (a ~ 1) & ( b,c: b,c: . a | b . a | b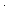 c c   a | b a | b 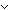 a | c) a | c) |
| | | Thm*  a: a: . prime(a) . prime(a) 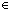 Prop Prop |
|
| not | Def 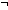 A == A A == A   False False |
| | | Thm*  A:Prop. ( A:Prop. (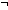 A) A) 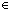 Prop Prop |
|
| prime_decider | Def is_prime(x) == prime_decider_exists{1:l}(x) |
| | | Thm*  x: x: . is_prime(x) . is_prime(x) 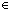 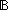 |