Thm*  n: n: , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: , z:{a...}, s:({a...z} , z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* (s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q) i.q)
Thm* ( 
Thm* ((2^n) z-a+1) z-a+1) | [hanoi_sol2_lb] |
Thm*  n: n: 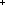 , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: , z:{a...}, s:({a...z} , z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* (s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q) i.q)
Thm* ( 
Thm* (( x:{a...z-1}, y:{x+1...z}, p',q':Peg. x:{a...z-1}, y:{x+1...z}, p',q':Peg.
Thm* ((( u:{a...x}. s(u,n) = p) & ( u:{a...x}. s(u,n) = p) & ( u:{y...z}. s(u,n) = q) u:{y...z}. s(u,n) = q)
Thm* ((& s(x) = ( i.p') i.p')  {1...n-1} {1...n-1}  Peg & s(y) = ( Peg & s(y) = ( i.q') i.q')  {1...n-1} {1...n-1}  Peg Peg
Thm* ((& p  p' p'
Thm* ((& q  q')) q')) | [hanoi_sol2_analemma] |
Thm*  n: n: , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: . .
Thm* (1of(HanoiSTD(n disks; from: p; to: q; indexing from: a)) = a+(2^n)-1) | [hanoi_general_exists_lemma2PROG_endpoint] |
Thm*  n: n: , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: . .
Thm* ( z:{a...}, s:({a...z} z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* (s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q)) i.q)) | [hanoi_sol2_via_general] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), a: Peg), a: . .
Thm*  z:{a...}, s:({a...z} z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g | [hanoi_general_exists] |
Thm*  n: n: , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: . .
Thm* (HanoiSTD(n disks; from: p; to: q; indexing from: a)/z,s.
Thm* (s is a Hanoi(n disk) seq on a..z
Thm* (& s(a) = ( i.p) i.p)  {1...n} {1...n}  Peg Peg
Thm* (& s(z) = ( i.q) i.q)  {1...n} {1...n}  Peg) Peg) | [hanoi_sol2_ala_generalPROGworks] |
Thm*  n: n: 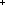 , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: . .
Thm* (HanoiSTD(n disks; from: p; to: q; indexing from: a)
Thm* (=
Thm* ((HanoiSTD(n-1 disks; from: p; to: otherPeg(p; q); indexing from: a)/m,s1.
Thm* ((HanoiSTD(n-1 disks; from: otherPeg(p; q); to: q; indexing from: m+1)
Thm* ((/z,s2. <z,HanoiHelper(n; s1;  i.p; s2; i.p; s2;  i.q)/r1,r2. r1 @(m) r2>)) i.q)/r1,r2. r1 @(m) r2>)) | [hanoi_sol2_ala_generalPROGcomp] |
Thm*  n: n: , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: . .
Thm* (HanoiSTD(n disks; from: p; to: q; indexing from: a)
Thm* ( z:{a...} z:{a...} ({a...z} ({a...z}  {1...n} {1...n}  Peg)) Peg)) | [hanoi_sol2_ala_generalPROG_wf] |
Thm*  n: n: , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: . .
Thm* ( z:{a...}, s:({a...z} z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* (s is a Hanoi(n disk) seq on a..z & s(a) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q)) i.q)) | [hanoi_sol2_ala_general] |
Thm*  n: n: , p,q:Peg. , p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( z:{1...}, s:({1...z} z:{1...}, s:({1...z}  {1...n} {1...n}  Peg). Peg).
Thm* (s is a Hanoi(n disk) seq on 1..z & s(1) = ( i.p) & s(z) = ( i.p) & s(z) = ( i.q)) i.q)) | [hanoi_sol2_via_permshift] |
Thm*  n: n: 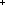 , a: , a: , z:{a...}, m:{a...z-1}, f,g:({1...n} , z:{a...}, m:{a...z-1}, f,g:({1...n}  Peg). Peg).
Thm* f(n)  g(n) g(n)
Thm*  
Thm* ( s1:({a...m} s1:({a...m}  {1...n-1} {1...n-1}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n-1} {1...n-1}  Peg). Peg).
Thm* (s1 is a Hanoi(n-1 disk) seq on a..m
Thm* (& s1(a) = f  {1...n-1} {1...n-1}  Peg Peg
Thm* (& s2 is a Hanoi(n-1 disk) seq on m+1..z
Thm* (& s2(z) = g  {1...n-1} {1...n-1}  Peg Peg
Thm* (& s1(m) = s2(m+1)
Thm* (& ( i:{1...n-1}. s1(m,i) i:{1...n-1}. s1(m,i)  f(n) & s2(m+1,i) f(n) & s2(m+1,i)  g(n)) g(n))
Thm* ( 
Thm* ((HanoiHelper(n; s1; f; s2; g)/r1,r2.
Thm* (((r1 @(m) r2) is a Hanoi(n disk) seq on a..z & r1(a) = f & r2(z) = g)) | [hanoi_general_exists_lemma2PROGworks] |
Thm*  n: n: 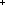 , a: , a: , z:{a...}, m:{a...z-1}, f,g:({1...n} , z:{a...}, m:{a...z-1}, f,g:({1...n}  Peg), Peg),
Thm*  s1:({a...m} s1:({a...m}  {1...n-1} {1...n-1}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n-1} {1...n-1}  Peg). Peg).
Thm* HanoiHelper(n; s1; f; s2; g)
Thm*  ({a...m} ({a...m}  {1...n} {1...n}  Peg) Peg) ({m+1...z} ({m+1...z}  {1...n} {1...n}  Peg) Peg) | [hanoi_general_exists_lemma2PROG_wf] |
Thm*  n: n: 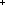 , a: , a: , z:{a...}, m:{a...z-1}, f,g:({1...n} , z:{a...}, m:{a...z-1}, f,g:({1...n}  Peg). Peg).
Thm* f(n)  g(n) g(n)
Thm*  
Thm* ( s1:({a...m} s1:({a...m}  {1...n-1} {1...n-1}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n-1} {1...n-1}  Peg). Peg).
Thm* (s1 is a Hanoi(n-1 disk) seq on a..m
Thm* (& s1(a) = f  {1...n-1} {1...n-1}  Peg Peg
Thm* (& s2 is a Hanoi(n-1 disk) seq on m+1..z
Thm* (& s2(z) = g  {1...n-1} {1...n-1}  Peg Peg
Thm* (& s1(m) = s2(m+1)
Thm* (& ( i:{1...n-1}. s1(m,i) i:{1...n-1}. s1(m,i)  f(n) & s2(m+1,i) f(n) & s2(m+1,i)  g(n))) g(n)))
Thm*  
Thm* ( r1:({a...m} r1:({a...m}  {1...n} {1...n}  Peg), r2:({m+1...z} Peg), r2:({m+1...z}  {1...n} {1...n}  Peg). Peg).
Thm* ((r1 @(m) r2) is a Hanoi(n disk) seq on a..z & r1(a) = f & r2(z) = g) | [hanoi_general_exists_lemma2] |
Thm*  n: n: 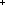 , f,g:({1...n} , f,g:({1...n}  Peg). Peg).
Thm* f(n) = g(n)
Thm*  
Thm* ( a: a: , z:{a...}. , z:{a...}.
Thm* (( s:({a...z} s:({a...z}  {1...n-1} {1...n-1}  Peg). Peg).
Thm* ((s is a Hanoi(n-1 disk) seq on a..z
Thm* ((& s(a) = f  {1...n-1} {1...n-1}  Peg Peg
Thm* ((& s(z) = g  {1...n-1} {1...n-1}  Peg) Peg)
Thm* ( 
Thm* (( s:({a...z} s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* ((s is a Hanoi(n disk) seq on a..z & s(a) = f & s(z) = g)) | [hanoi_general_exists_lemma1] |
Thm*  n: n: , a,z: , a,z: , m:{a...z-1}, s1:({a...m} , m:{a...z-1}, s1:({a...m}  {1...n} {1...n}  Peg), Peg),
Thm*  s2:({m+1...z} s2:({m+1...z}  {1...n} {1...n}  Peg). Peg).
Thm* ( k:{1...n}. Moving disk k of n takes s1(m) to s2(m+1)) k:{1...n}. Moving disk k of n takes s1(m) to s2(m+1))
Thm*  
Thm* s1 is a Hanoi(n disk) seq on a..m
Thm*  
Thm* s2 is a Hanoi(n disk) seq on m+1..z
Thm*  
Thm* (s1 @(m) s2) is a Hanoi(n disk) seq on a..z | [hanoi_seq_join_seq] |
Thm*  n: n: , m,a,z: , m,a,z: , s1:({a...m} , s1:({a...m}  {1...n} {1...n}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n} {1...n}  Peg), Peg),
Thm*  x:{m+1...z}. (s1 @(m) s2)(x) = s2(x) x:{m+1...z}. (s1 @(m) s2)(x) = s2(x) | [hanoi_seq_join_part2] |
Thm*  n: n: , m,a,z: , m,a,z: , s1:({a...m} , s1:({a...m}  {1...n} {1...n}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n} {1...n}  Peg), Peg),
Thm*  x:{a...m}. (s1 @(m) s2)(x) = s1(x) x:{a...m}. (s1 @(m) s2)(x) = s1(x) | [hanoi_seq_join_part1] |
Thm*  n: n: , m,a,z: , m,a,z: , s1:({a...m} , s1:({a...m}  {1...n} {1...n}  Peg), s2:({m+1...z} Peg), s2:({m+1...z}  {1...n} {1...n}  Peg). Peg).
Thm* (s1 @(m) s2)  {a...z} {a...z}  {1...n} {1...n}  Peg Peg | [hanoi_seq_join_wf] |
Thm*  n': n': , n:{n'...}, a: , n:{n'...}, a: , z:{a...}, s:({a...z} , z:{a...}, s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z
Thm*  
Thm* ( x:{a...z}, i:{n'+1...n}. s(a,i) = s(x,i)) x:{a...z}, i:{n'+1...n}. s(a,i) = s(x,i))
Thm*  
Thm* s is a Hanoi(n' disk) seq on a..z | [hanoi_seq_shallower] |
Thm*  n: n: , a,z: , a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z
Thm*  
Thm* ( a',z':{a...z}. s is a Hanoi(n disk) seq on a'..z') a',z':{a...z}. s is a Hanoi(n disk) seq on a'..z') | [hanoi_subseq] |
Thm*  n: n: , a,z,d: , a,z,d: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z
Thm*  
Thm* ( x.s(x-d)) is a Hanoi(n disk) seq on a+d..z+d x.s(x-d)) is a Hanoi(n disk) seq on a+d..z+d | [hanoi_seq_shift] |
Thm*  a,z: a,z: , n: , n: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg), n': Peg), n': . .
Thm* n n' n'
Thm*  
Thm* ( h:({n+1...n'} h:({n+1...n'}  Peg). Peg).
Thm* (s is a Hanoi(n disk) seq on a..z
Thm* ( 
Thm* ((s(?) {to n}  h {to n'}) is a Hanoi(n' disk) seq on a..z) h {to n'}) is a Hanoi(n' disk) seq on a..z) | [hanoi_seq_deepen_seq] |
Thm*  a,z: a,z: , n: , n: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg), n': Peg), n': . .
Thm* n n' n'
Thm*  
Thm* ( h:({n+1...n'} h:({n+1...n'}  Peg), i:{1...n'}. Peg), i:{1...n'}.
Thm* (i n n   ( ( x:{a...z}. (s(?) {to n} x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = s(x,i))) h {to n'})(x,i) = s(x,i))) | [hanoi_seq_deepen_loweq] |
Thm*  a,z: a,z: , n: , n: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg), n': Peg), n': . .
Thm* n n' n'
Thm*  
Thm* ( h:({n+1...n'} h:({n+1...n'}  Peg), i:{1...n'}. Peg), i:{1...n'}.
Thm* (n<i   ( ( x:{a...z}. (s(?) {to n} x:{a...z}. (s(?) {to n}  h {to n'})(x,i) = h(i))) h {to n'})(x,i) = h(i))) | [hanoi_seq_deepen_higheq] |
Thm*  a,z: a,z: , n: , n: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg), n': Peg), n': . .
Thm* n n' n'
Thm*  
Thm* ( h:({n+1...n'} h:({n+1...n'}  Peg). (s(?) {to n} Peg). (s(?) {to n}  h {to n'}) h {to n'})  {a...z} {a...z}  {1...n'} {1...n'}  Peg) Peg) | [hanoi_seq_deepen_wf] |
Thm*  n: n: , a,z: , a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z
Thm*  
Thm* ( f:(Peg f:(Peg  Peg). Peg).
Thm* (Inj(Peg; Peg; f)   ( ( x,i. f(s(x,i))) is a Hanoi(n disk) seq on a..z) x,i. f(s(x,i))) is a Hanoi(n disk) seq on a..z) | [hanoi_seq_permutepegs] |
Thm*  n': n': , n:{n'...}, a,z: , n:{n'...}, a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z
Thm*  
Thm* ( a',z':{a...z}. a',z':{a...z}.
Thm* (( x:{a'...z'}, i:{n'+1...n}. s(a',i) = s(x,i)) x:{a'...z'}, i:{n'+1...n}. s(a',i) = s(x,i))
Thm* ( 
Thm* (s is a Hanoi(n' disk) seq on a'..z') | [hanoi_seq_core] |
Thm*  n: n: , a,z: , a,z: , s:({a...z} , s:({a...z}  {1...n} {1...n}  Peg). Peg).
Thm* s is a Hanoi(n disk) seq on a..z  Prop Prop | [hanoi_seq_wf] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Thm* Moving disk k of n takes f to g   f(k) f(k)  g(k) g(k) | [hanoi_step_at_diff] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Thm* Moving disk k of n takes f to g   Moving disk k of n takes g to f Moving disk k of n takes g to f | [hanoi_step_at_sym] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), j:{1...n}. Peg), j:{1...n}.
Thm* ( k:{1...n}. Moving disk k of n takes f to g) k:{1...n}. Moving disk k of n takes f to g)
Thm*  
Thm* f(j)  g(j) g(j)   Moving disk j of n takes f to g Moving disk j of n takes f to g | [hanoi_step_at_change] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), i,k:{1...n}. Peg), i,k:{1...n}.
Thm* Moving disk k of n takes f to g   f(i) f(i)  g(i) g(i)   i = k i = k | [hanoi_step_at_unique] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Thm* Moving disk k of n takes f to g
Thm*  
Thm* f = ( i.otherPeg(f(k); g(k))) i.otherPeg(f(k); g(k)))  {1...k-1} {1...k-1}  Peg Peg | [hanoi_step_at_otherpeg] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Thm* Moving disk k of n takes f to g   f(k) f(k)  g(k) g(k) | [hanoi_step_at_change2] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k,i:{1...n}. Peg), k,i:{1...n}.
Thm* Moving disk k of n takes f to g   i i  k k   f(i) = g(i) f(i) = g(i) | [hanoi_step_at_same] |
Thm*  n: n: , f,g:({1...n} , f,g:({1...n}  Peg), k:{1...n}. Peg), k:{1...n}.
Thm* Moving disk k of n takes f to g  Prop Prop | [hanoi_step_at_wf] |
Thm*  n: n: , f:({1...n} , f:({1...n}  Peg), n': Peg), n': . .
Thm* n n' n'
Thm*  
Thm* ( f':({n+1...n'} f':({n+1...n'}  Peg), i:{1...n'}. Peg), i:{1...n'}.
Thm* (n<i   (f {to n} (f {to n}  f' {to n'})(i) = f'(i)) f' {to n'})(i) = f'(i)) | [hanoi_extend_higheq] |
Thm*  n: n: , f:({1...n} , f:({1...n}  Peg), n': Peg), n': . .
Thm* n n' n'
Thm*  
Thm* ( f':({n+1...n'} f':({n+1...n'}  Peg), i:{1...n'}. Peg), i:{1...n'}.
Thm* (i n n   (f {to n} (f {to n}  f' {to n'})(i) = f(i)) f' {to n'})(i) = f(i)) | [hanoi_extend_loweq] |
Thm*  n: n: , f:({1...n} , f:({1...n}  Peg), n': Peg), n': . .
Thm* n n' n'   ( ( f':({n+1...n'} f':({n+1...n'}  Peg). (f {to n} Peg). (f {to n}  f' {to n'}) f' {to n'})  {1...n'} {1...n'}  Peg) Peg) | [hanoi_extend_wf] |
Thm*  p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   permute(p to r ; q to s)(q) = s permute(p to r ; q to s)(q) = s | [hanoi_peg_perm_comp2] |
Thm*  p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   permute(p to r ; q to s)(p) = r permute(p to r ; q to s)(p) = r | [hanoi_peg_perm_comp1] |
Thm*  p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   Inj(Peg; Peg; permute(p to r ; q to s)) Inj(Peg; Peg; permute(p to r ; q to s)) | [hanoi_peg_perm_is_inj] |
Thm*  p,r,q,s:Peg. p p,r,q,s:Peg. p  q q   r r  s s   permute(p to r ; q to s) permute(p to r ; q to s)  Peg Peg  Peg Peg | [hanoi_peg_perm_wf] |
Thm*  x,y:Peg. x x,y:Peg. x  y y   y y  otherPeg(x; y) otherPeg(x; y) | [hanoi_otherpeg_diff4] |
Thm*  x,y:Peg. x x,y:Peg. x  y y   x x  otherPeg(x; y) otherPeg(x; y) | [hanoi_otherpeg_diff3] |
Thm*  x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) otherPeg(x; y)  y y | [hanoi_otherpeg_diff2] |
Thm*  x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) otherPeg(x; y)  x x | [hanoi_otherpeg_diff1] |
Thm*  x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) = otherPeg(y; x) otherPeg(x; y) = otherPeg(y; x) | [hanoi_otherpeg_sym] |
Thm*  x,y,z:Peg. x x,y,z:Peg. x  y y   x x  z z   y y  z z   x = otherPeg(y; z) x = otherPeg(y; z) | [hanoi_otherpeg_only] |
Thm*  x,y:Peg. x x,y:Peg. x  y y   otherPeg(x; y) otherPeg(x; y)  Peg Peg | [hanoi_otherpeg_wf] |
Thm*  p,q:Peg. p,q:Peg.
Thm* p  q q
Thm*  
Thm* ( a: a: , z:{a...}, f:({a...z} , z:{a...}, f:({a...z}  Peg). Peg).
Thm* (f(a) = p & f(z) = q
Thm* ( 
Thm* (( x:{a...z-1}, y:{x+1...z}. x:{a...z-1}, y:{x+1...z}.
Thm* ((( u:{a...x}. f(u) = p) u:{a...x}. f(u) = p)
Thm* ((& f(x+1)  p p
Thm* ((& f(y-1)  q q
Thm* ((& ( u:{y...z}. f(u) = q))) u:{y...z}. f(u) = q))) | [hanoi_pegseq_analemma] |
Thm*  p,q:Peg. (p= p,q:Peg. (p=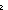 q) q)  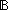 | [eq_hanoi_PEG_wf] |
Def Moving disk k of n takes f to g
Def == ( i:{1...n}. f(i) = g(i) i:{1...n}. f(i) = g(i)  Peg Peg 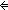  i i  k) k)
Def == & ( i:{1...k-1}. f(i) i:{1...k-1}. f(i)  f(k) f(k)  Peg & g(i) Peg & g(i)  g(k) g(k)  Peg) Peg) | [hanoi_step_at] |